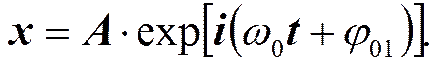Экспоненциальная форма представления колебаний
Для того чтобы ввести новый вид записи колебаний необходимо разобраться с комплексными числами. Комплексным числом z называется число следующего вида.
где x и y – вещественные числа, а i – мнимая единица ( Число x называется вещественной частью комплексного числа z. Символически это записывается в следующем виде x = Re z. Число y называется мнимой частью числа z (записывается: y = Im z). Число
называется комплексно сопряжённым числу Вещественному числу x можно сопоставить точку на оси x. Комплексному числу z можно сопоставить точку на плоскости, имеющую координаты x, y. Каждая точка плоскости определяет некоторое комплексное число z. Следовательно, комплексное число можно задать в виде (1) с помощью декартовых координат x и y соответствующей точки. То же самое число можно задать с помощью полярных координат r и a. Между этими парами координат имеются следующие соотношения.
Расстояние от начала координат до точки, изображающей число z, называется модулем комплексного числа и обозначается | z |.
Число a называется аргументом комплексного числа z. Приняв во внимание все соотношения (3), можно представить комплексное число в тригонометрической форме.
Два комплексных числа, z1 = z2, если x1 = x2 и y1 = y2. (6) Модули двух равных между собой комплексных чисел одинаковы, а аргументы могут различаться лишь слагаемым, кратным 2 p.
Из выражений (1) и (2) видно, что в случае, когда z* = z, мнимая часть z есть нуль, т.е. число z оказывается чисто вещественным. Таким образом, условия вещественности числа z можно записать в следующем виде.
В математике доказывается следующее соотношение.
Это выражение называется формулой Эйлера. Заменив в этой формуле a на –a и учтя, что cos(–a) = cosa, а sin(–a) = –sin(a), получим следующее соотношение.
Сложим (9) и (10) и решим получившееся соотношение относительно cosa. В результате получим.
Вычтем (10) из (9) и получим.
С помощью формулы (9) комплексное число можно записать в показательной форме.
См. (5) и (9). Тогда комплексно сопряжённое число в показательной форме будет иметь следующий вид.
Общее решение уравнения гармонических колебаний имеет вид.
Воспользовавшись формулой Эйлера (9) то же самое можно записать следующим образом.
Или как чаще записывают, подразумевая только вещественную часть.
|

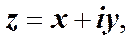 (1)
(1) ).
).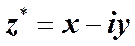 (2)
(2) .
.
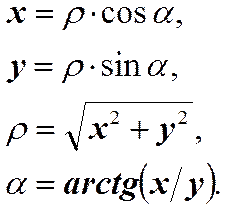 (3)
(3)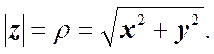 (4)
(4)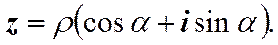 (5)
(5)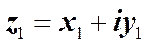 и
и 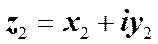 , считаются равными друг другу, если в отдельности равны их вещественные и мнимые части.
, считаются равными друг другу, если в отдельности равны их вещественные и мнимые части.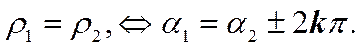 (7)
(7)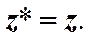 (8)
(8) (9)
(9)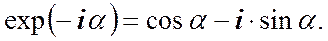 (10)
(10)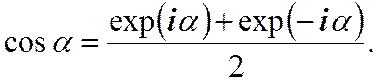 (11)
(11)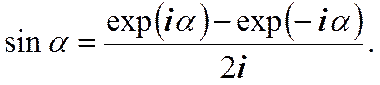
 (12)
(12)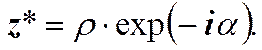 (13)
(13)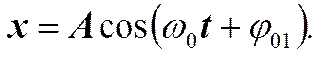 (14)
(14)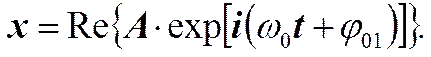 (15)
(15)