Вынужденные электрические колебания
Это напряжение нужно прибавить к э.д.с. самоиндукции в исходной формуле для затухающих колебаний. Рассмотрим этот вопрос кратко используя аналогию с механическими колебаниями.
Уравнение вынужденных электрических колебаний имеет вид.
Мы имеем уже известное нам неоднородное линейное дифференциальное уравнение вынужденных колебаний. Решение неоднородного дифференциального уравнения представим в виде его частного решения для установившихся колебаний. Это решение, как и для механических вынужденных колебаний, имеет вид:
где Выражения для постоянных величин
Если подставить значения
С использованием соотношений для постоянных величин - напряжение на емкости отстает по фазе от тока на угол - напряжение на активном сопротивлении изменяется в фазе с током; - напряжение на индуктивности опережает по фазе ток на угол Величина называется полным сопротивлением цепи (или импеданс). Величина При последовательном соединении L, C, R, при X = 0 ( На конденсаторе напряжение достигает максимума при круговой частоте равной
Полное сопротивление Z = R и тогда U = UR, а UC и UL одинаковы по величине и противоположны по фазе.
Такой вид резонанса называется резонансом напряжений или последовательным резонансом. Можно записать.
Т.е. при резонансе на ёмкости можно получить напряжение с амплитудой
Ниже приведены графики зависимостей напряжения на конденсаторе и тока через индуктивность (напряжения на резисторе) от частота. В цепях переменного тока содержащих параллельно включённые ёмкость и индуктивность наблюдается другой тип резонанса.
Для тока через ёмкость имеем.
При R = 0 и L = 0
где n = 1, 2, 3,... Аналогично для тока через индуктивность.
При R = 0 и С = ¥; (условие отсутствия ёмкости в цепи).
где n = 1, 2, 3,... Из (7) и (8) вытекает, разность фаз токов в разных ветвях цепи будет равна
По первому правилу Кирхгофа I = I1 + I2. Тогда для амплитудных значений можно записать.
Если Явление резкого уменьшения тока во внешней цепи при приближении частоты w приложенного напряжения к резонансной частоте wрез называется резонансом токов или параллельным резонансом. Это свойство используется в резонансных усилителях и фильтрах. Ниже приведён график зависимости тока во внешней цепи от частоты внешней э.д.с.
|

 Для компенсации потерь в колебательном контуре нужно оказывать на контур периодически изменяющееся воздействие. Это можно осуществить, например, включив последовательно с элементами контура переменную э.д.с. или, разорвав контур, подать на образовавшиеся контакты переменное напряжение.
Для компенсации потерь в колебательном контуре нужно оказывать на контур периодически изменяющееся воздействие. Это можно осуществить, например, включив последовательно с элементами контура переменную э.д.с. или, разорвав контур, подать на образовавшиеся контакты переменное напряжение. 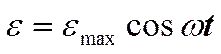 (1)
(1)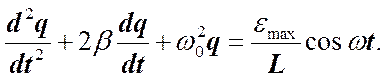 (2)
(2)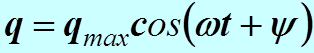 , (3)
, (3)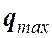 амплитуда заряда на конденсаторе;
амплитуда заряда на конденсаторе; 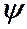 (пси) – разность фаз между колебаниями заряда и внешней э.д.с.
(пси) – разность фаз между колебаниями заряда и внешней э.д.с.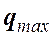 и
и 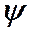 , как и для механических колебаний, запишем без вывода:
, как и для механических колебаний, запишем без вывода: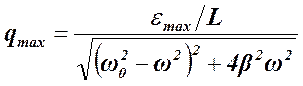 , (4)
, (4) и
и  , получим выражения для этих величин, записанные через параметры контура:
, получим выражения для этих величин, записанные через параметры контура: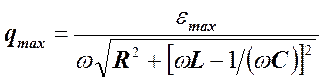 ,
, 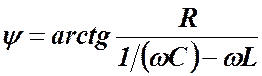 (5)
(5)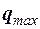 и
и 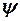 можно провести анализ параметров вынужденных колебаний в контуре. Как и в случае затухающих свободных колебаний ограничимся лишь общими выводами о сдвиге фаз колебаний тока и напряжения на элементах контура. Эти выводы следующие:
можно провести анализ параметров вынужденных колебаний в контуре. Как и в случае затухающих свободных колебаний ограничимся лишь общими выводами о сдвиге фаз колебаний тока и напряжения на элементах контура. Эти выводы следующие: ;
;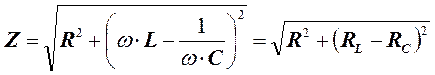 (6)
(6)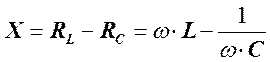 называется реактивным сопротивлением цепи.
называется реактивным сопротивлением цепи. ) наблюдается резонанс напряжений. При этом угол сдвига фаз между током и напряжением обращается в нуль.
) наблюдается резонанс напряжений. При этом угол сдвига фаз между током и напряжением обращается в нуль.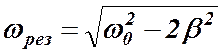 .
.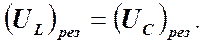
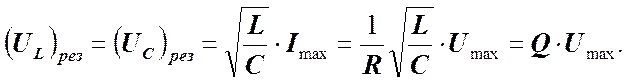
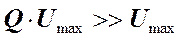 в узком диапазоне частот. Это свойство используется в усилителях напряжения.
в узком диапазоне частот. Это свойство используется в усилителях напряжения.
 Сопротивление контура мало R = 0.
Сопротивление контура мало R = 0.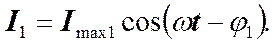 (7)
(7)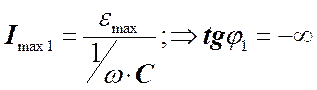 , т.е.
, т.е. 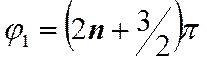 ,
,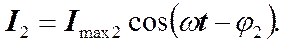 (8)
(8)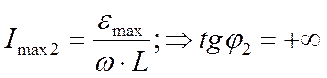 , т.е.
, т.е. 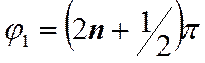 ,
,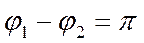 , т.е. токи в этих цепях противоположны по фазе.
, т.е. токи в этих цепях противоположны по фазе.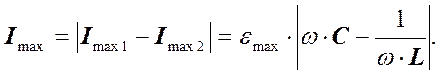 (9)
(9)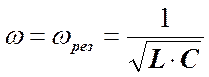 , то Imax1 = Imax2 и Imax = 0.
, то Imax1 = Imax2 и Imax = 0.



