Переменный электрический ток
Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи, обладающей ёмкостью, индуктивностью и активным сопротивлением R, переменного тока. Под действием внешнего напряжения (оно играет роль внешней э.д.с. e)
Ток в цепи изменяется по закону:
Задача сводится к определению амплитуды силы тока и сдвига тока по фазе относительно напряжения U. Полученное выражение для амплитуды силы тока Imax(w) можно формально трактовать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе выражения (3) величину, имеющую размерность сопротивления, называют полным сопротивлением или импедансом.
Видно, что при
При этом величину w×L называют индуктивным сопротивлением и обозначают следующим образом.
Величину
Заметим, что индуктивное сопротивление растёт с увеличением частоты w, а ёмкостное сопротивление – уменьшается. Когда говорят, что в цепи отсутствует ёмкость, то это надо понимать в смысле отсутствия ёмкостного сопротивления, которое равно Важно отметить. Хотя реактивное сопротивление измеряют в тех же единицах, что и активное сопротивление, между ними существует принципиальное отличие. Оно заключается в том, что только активное сопротивление определяет необратимые процессы в цепи, такие, например, как преобразование электромагнитной энергии в джоулеву теплоту. Рассмотрим мощность, выделяемую в цепи переменного тока. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока.
Воспользуемся формулой
Учтём и запомним на будущее, что
Это выражение можно привести к другому виду, если рассмотреть векторную диаграмму.
Из векторной диаграммы следует, что  . Поэтому получим. . Поэтому получим.
Такую же мощность развивает ток Величины называются действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуированы по действующим значениям тока и напряжения. Выражение средней мощности (8) переписанное через действующие значения напряжения и тока имеет следующий вид.
Множитель cosj называется коэффициентом мощности. Таким образом, выделяемая в цепи мощность зависит не только от напряжения и силы тока, но и от сдвига фаз между током и напряжением.
При j = p/2 значение Зависимость мощности от cosj необходимо учитывать при проектировании линий электропередачи на переменном токе. Если питаемые нагрузки имеют большое реактивное сопротивление X, то cosj может быть заметно меньше единицы. В этих случаях для передачи потребителю нужной мощности (при данном напряжении генератора) необходимо увеличивать ток I, а это приводит к возрастанию бесполезных потерь энергии в подводящих проводах. Поэтому нужно всегда распределять нагрузки, индуктивности и ёмкости так, чтобы cosj был по возможности близок к единице. Для этого достаточно сделать реактивное сопротивление X как можно меньше, т.е. обеспечить равенство индуктивного и ёмкостного сопротивлений (RL = RC). В заключение заметим, что понятие активного сопротивления шире, чем понятие электрического сопротивления проводников, образующих цепь. Последнее обуславливает переход энергии тока только в джоулеву теплоту, но возможны и другие превращение этой энергии, например, в механическую работу (электромоторы). Активное сопротивление тогда уже не сводится к электрическому сопротивлению, а обычно превосходит его.
|

 . (1)
. (1) (2)
(2)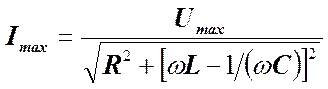 ,
,  (3)
(3) . (4)
. (4) это сопротивление минимально и равно активному сопротивлению R. Величину, стоящую в круглых скобках формулы (4) называют реактивным сопротивлением.
это сопротивление минимально и равно активному сопротивлению R. Величину, стоящую в круглых скобках формулы (4) называют реактивным сопротивлением. (5)
(5)
 называют ёмкостным сопротивлением.
называют ёмкостным сопротивлением. (6)
(6) и, следовательно, обращается в нуль, если
и, следовательно, обращается в нуль, если  (при замене конденсатора закороченным участком цепи).
(при замене конденсатора закороченным участком цепи).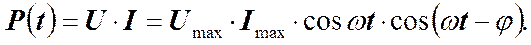 (7)
(7) и преобразуем (7) к следующему виду.
и преобразуем (7) к следующему виду. Практическое значение имеет среднее за период колебание значения мощности.
Практическое значение имеет среднее за период колебание значения мощности.
 ,
, . Получим.
. Получим. (8)
(8)
 (9)
(9) .
. ,
, 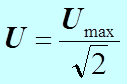 (10)
(10) (11)
(11) , какими бы не были величины U и I. В этом случае энергия, передаваемая за четверть периода от генератора во внешнюю цепь, в точности равна энергии, передаваемой из внешней цепи в генератор в течение следующей четверти периода, и вся энергия бесполезно "колеблется" между генератором и внешней цепью.
, какими бы не были величины U и I. В этом случае энергия, передаваемая за четверть периода от генератора во внешнюю цепь, в точности равна энергии, передаваемой из внешней цепи в генератор в течение следующей четверти периода, и вся энергия бесполезно "колеблется" между генератором и внешней цепью.


