In one direction
It is necessary be able to determine the stresses acting at any inclined section of a tensed (compressed) element. To conclude about the material strength (Fig. 2.6).
Fig.2.6.
Consider the normal stresses at the bar Let us determine the stresses arising at the inclined BC section with the normal to it under the Denote: A is the cross-area perpendicular to the bar axis; Аα is the inclined cross area herewith
Using the relation (2.1) we find
Projecting the forces on the
then
With The given direction of the shearing stress is characterized by the necessity to rotate the external n normal to the section area clockwise to coincide with the shearing stress. The shearing stresses of this direction are considered positive (are thought positive). If it is necessary to rotate the normal to the area against the clock to coincide with the shearing stress, this stress is then considered negative (Fig. 2.6 c). From formula (2.3) it follows that the maximum values of the normal stresses are set up under From formula (2.4) it follows that under From formulae (2.3) and (2.4) it is evident that under Thus, the longitudinal sections have neither normal nor shearing stresses. The areas having no shearing stresses are called principal areas and the normal stresses acting along them are the principal stresses. Consequently, the normal stress at the cross section for the tensed or compressed bar is the principal one. It is also evident from formula (2.4) that the maximum shearing stress takes place at the section under
|


 cross section to be known (for example
cross section to be known (for example 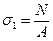 ).
). angle of the
angle of the  (2.1)
(2.1) normal and
normal and  shear stresses act at the inclined section in general case. We determine their values from the equilibrium condition, for example of the cut low part (Fig. 2.6 b). Project the forces on the
shear stresses act at the inclined section in general case. We determine their values from the equilibrium condition, for example of the cut low part (Fig. 2.6 b). Project the forces on the  direction:
direction: . (2.2)
. (2.2) (2.3)
(2.3)
 (2.4)
(2.4) value positive, (i.e. tension) and at 0 ≤
value positive, (i.e. tension) and at 0 ≤  = 0 the shearing stress is equal to zero.
= 0 the shearing stress is equal to zero. = 0 and
= 0 and  = 0.
= 0. (2.5)
(2.5)


