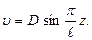Stability analysis of the bars in compression (buckling).
Stable and unstable equilibrium forms
It is known from theoretical mechanics that the equilibrium of the absolutely rigid body can be stable, indifferent and unstable. For example, a ball lying on the concave surface is in the stable equilibrium state. If a small deviation of this position is made and then released, it returns into its original position (Fig. 9.1 a). The ball lying on the horizontal surface is in the indifferent equilibrium state (Fig. 9.1 b).
а) b) c)
Fig. 9.1.
It does not return to original position being deviated but its movement will stop. At last the ball lying on the convex surface is in the unstable equilibrium state (Fig. 9.1 c). It continues to move further being deviated from the original state. Analogous examples can be given from the equilibrium region of the deforming bodies. So, the long bar under the action of the comparatively small axial compression force (lesser than some critical value) is in the stable equilibrium state (Fig. 9.2 a). If some lateral load bends the bar insignificantly, it straightens again and receives the original equilibrium shape. The bended shape of the bar equilibrium in this case turns out unstable and because of it impossible. Under the value of the compressive force greater than some critical value, on the contrary, the rectilinear equilibrium shape becomes unstable, so it is replaced by the deflected position of the equilibria that occurs to be stable (Fig.9.2 c).
Fig. 9.2. The minimum value of the compressive force under which the compressive bar loses the ability to keep the rectilinear equilibrium shape is called the critical force and denoted Fcr (Fig. 9.2 b). By Euler’s definition the force which is needed to incline slightly the column is called the critical force. The considered scheme of the axial compressive bar has some theoretic character. In practice it is necessary to take into account the fact that the compressive force can act with some eccentricity and the bar can have some (very slight) initial curvature. So, some bending of the bar is observed right from the start of the longitudinal loading. Special investigations show that while the compressive force is lesser than the critical one, the bar defection will be small but, when the force value approaches to its critical value they begin to increase quickly (Fig. 9.2 c). This criterion (theoretically unlimited growth of the defection under the unlimited growth of the compressive force) can be accepted as a criterion of lateral buckling. Practically the bar will be broken earlier as the result of exhausting the material strength. Having determined the critical force it is necessary to obtain the allowable loading for the compressive bar. For safety the allowable load, naturally, must be lesser than the critical:
where nsis the safety factor of stability. The accepted safety factor of stability is such as to ensure the reliable work of the bar in spite of the fact that the real condition of its work can be less favorable than the conditions accepted for the design (because of heterogeneity materials, inexactitudes in determining loads and so on). Then the safety factor of stability is accepted to be some more than the assurance coefficient because there are additional unfavorable circumstances: the initial bar curvature, the possible load action eccentricity and others. For steel the normative safety factor of stability ns is in the limits from 1.8 to 3, for cast-iron is from 5 to 5.5, for wood is from 2.8 to 3.2. The pointed values of the safety factor of stability are accepted when designing the building constructions. The values accepted when when designing the machine-building construction elements (for example the lead screw of the metal-working machine) are larger; so for steel they are ns= 4-5. To take into account certain working conditions of the of compressive bars it is recommended to apply a system of particular coefficients, not one. The elastic equilibrium loss of stability can also be in torsion, bending and combined deformations. The analyses show that the loss of stability was the cause of numerous catastrophes and constructure failures.
9.2. Euler’s formula for the critical force
Let us consider the bar in a critical state when the compressive force achieves the critical value i.e. accept that the bar is slightly bent (Fig. 9.3). If the moments of inertia about two principal central axes of the cross section are not equal, then the elastic buckling will be in the minimum rigid plane i.e. the cross section will about the axis whose inertia moment has the minimum. It is easyto see while compressing the flexible ruler. To study the elastic buckling and to determine the critical force let’s use the approximate differential equation of the deflection curve of the bent beam
The bending moment about the section centroid in a bent bar state is
Fig. 9.3.
The minus sign is taken because the bar is bent with a concave downward while the deflection
Denoting
we get
It is the linear differential equation of a second order. Its general solution as it is well known from mathematics looks like
Here C and D are constants of integration, to determine these we impose the boundary conditions at the bar ends: 1) at 2) at From the first condition we get C = 0. Hence, the bar is bent by the sine curve The first case D = 0. But if C = 0 and D = 0 as follows from the equation (9.5), the bar deflections are equal to zero, which contradicts the original precondition. The second case sin Thus we get a countless values number of critical forces corresponding to different shapes of a curved bar. From a practical point of view the interest is but the minimum value of the critical force when the bar loses its stability. The first root n = 0 does not give the solution to the problem. Under n = 1 we receive the minimum value of the critical force:
This is Euler’s formula. The bar bend along the sine curve with one-half wave corresponds to the critical force, i.e.
The next roots give the large values of the critical force, which we will not consider. The bar bend along the sine curve with some half-waves which will be received if the bend along the sine curve with a half-wave is for some reason impossible (for example, because of the intermediate ties existence) corresponds these roots. It should be kept in mind that the constant D, hence the shape of the bar bend axis proper were indeterminate. When applying for the research of the elastic buckling not an approximate but the exact differential equation of the bend axis, it is possible to determine both the critical force value and the relation between the compressing force and the bar deflection.
|



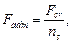 (9.1)
(9.1) (9.2)
(9.2) (9.3)
(9.3)
 is positive. If the bar was bent with a concave downward, the deflection v would get the same result. Considering (9.2) the equation (9.3) becomes
is positive. If the bar was bent with a concave downward, the deflection v would get the same result. Considering (9.2) the equation (9.3) becomes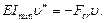
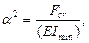
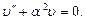 (9.4)
(9.4) (9.5)
(9.5)
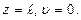
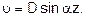 From the second condition we get
From the second condition we get 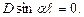 This relation is true for two cases.
This relation is true for two cases. This condition is performed when
This condition is performed when  accepts the following infinite value series:
accepts the following infinite value series:  where n is any whole number. From this
where n is any whole number. From this 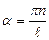 and since
and since 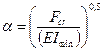 ,
, 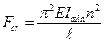 .
. (9.6)
(9.6)