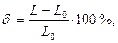Practicum
Laboratory work № 1
“Testing materials in axial tension. Defining basic mechanical characteristics of the material”
Introduction
When designing machines, mechanisms, pipelines, reservoirs, building constructions it is necessary to know the values characterizing the strength and deformative properties of materials. The values can be received by mechanical testing carried out in specially equipped laboratories by testing machines. There is a variety of such tests: the hardness test, the resistibility to impact, variable loads test and so on. But tension and compression tests are the main. The purpose of the present paper is to study the material behavior in the process of the tension test and to define its mechanical characteristics, namely the module of elasticity (Young's modulus) E, the proportional limit
Theory
Stresses and deformation. The behaviour of metals under the action of external forces is characterized by their mechanical properties which permit to define the limits of load for each material, to value different materials correlatively and to verify the metals quality in factory and laboratory conditions. By mechanical properties we mean the characteristics defining the behaviour of a metal (or some other material) under the action of external mechanical forces applied. The force action causes the deformation of a hard body, stresses arise within it. The stress is the ultimate value. In the simplest case of the axially loaded bar (fig. 1, a) the stress is the force acting over the unit area of the cross section:
where P is the stress over the cross section by the area A, perpendicular to the specimen axis, along which the force F acts. In the SI system stresses are expressed by units N/m2, Pa or MN/m2 i.e. MPa. It had been formerly put into practice that a unit is kgf/mm2 (1 kgf/mm2 = 9.81 MPa). In a general case the force is not perpendicular to the section plane it acts upon. Then, according to the vector rules, the force can be decomposed into two components: a normal force (perpendicular to the section plane), making a normal stress and a shearing force, acting in the tangential direction to the plane and creating a shearing stress (Fig. 1 b, c). These stresses are determined by the mechanical testing of materials. Also the same tests are used to determinate the efforts necessary for the treatment of metals by pressure and to calculate the strength. It is due to the fact that at deformations and ruptures some processes are determined by shearing stresses (plastic deformation, shear rupture), others by normal stresses (tension rupture). From Fig. 1,c it follows that the resultant stress P acting in the shaded area of the section
Since
Thus, the normal stress in the section
and the shearing stress is
From equations it follows that the maximum normal stresses in the axially loaded bar arise at a=0 i.e. at the plane perpendicular to the tension axis and the maximum shearing stresses arise at a=45°. Normal stresses are subdivided into tension (positive) and compression (negative) ones. Stresses used in mechanical testing can be true and conditional. It is known that the area value, where stresses act (the cross sectional area of the sample), changes in the deformation process. If these changes are not taken into consideration, and the stresses are valued as the ratio of the current load to the initial cross sectional area, the stresses are called conditional. If the stress is the ratio of the force to the fact value of the section at the deformation moment, then the stresses are called true. Only true stresses have a physical meaning but in practice conditional stresses are more convenient to use.
Fig. 1. Formation of normal a and shearing t stresses in cases of applying the force F to the area A: a - the force is perpendicular to the section; b, c - the force is not perpendicular to the section.
Under the action of external loads, the body is deformed, as the result its form and dimensions may change. A deformation is termed elastic if it disappears after the load is entirely removed. Under the elastic deformation there is a reverse atoms displacement from equilibrium of the crystalline space. Elastic deformation does not cause either a visible residual changes of the structure or the property of a metal. The removed atoms under the action of repulsion (in compression) are returned to the initial position, when the load is removed and bodies receive the initial form and dimensions. Elastic properties of materials are determined by forces of atoms interactions. When shearing stresses increase over a certain value the deformation remains unreversible even if the load is removed. Plastic deformation is based on the unreverse displacement of one parts of the crystal relatively to others. Only elastic component of the deformation disappears if the load is removed and the plastic deformation remains. Therefore the structure of metals is changed under the permanent deformation unreversely and consequently its properties are changed too. The plastic deformation is realized by slipping and doubling, whose basis is the dislocation mechanism of a deformation. A deformation can be finished by a rupture under the corresponding conditions of loading i.e. by full or partial breaking of the body continuance.
The basic stages of the deformation process. We can imagine different stages of the deformation process better if we consider the diagram of a body deformation under the action of the increasing load. This diagram is usually plotted with the test results in "deformation - force" coordinates (fig.2). For metals and their alloys the deformation process under the action of a gradually increasing load (static loads) consists of three stages, superposable each other. 1. The stage of elastic deformations (up to point A); the relation between the force and the strain is determined by Hooke’s law and it depends on material elastic properties. 2. The stage of elastoplastic deformations (portion AB); the relation between the force and the strain is determined by a curve, whose character depends on material properties, loading conditions and the choice of coordinates of the deformation diagram. 3. The stage of breaking (portion BC); this rupture in a deformation process is conditional, because it is impossible to differentiate between the described stages. For instance, a plastic deformation of private grains of a polycrystal metal can be found by metallographic and X-ray methods for the area with practically a linear relation between a force and deformation i.e. the microscopic elastic range. This deformation heterogeneity is also conserved for the plastic area. Therefore long before the entire rupture rupture cracks can be found there. However the distribution of the deformation process indicated above is necessary and appropriate, as it delimits the basic behavioural patterns of materials under a mechanical loading. Mechanical properties of materials: strength, hardness, plasticity, viscosity, elasticity are determined under different conditions of loading and at different sequences of efforts application. Testing materials in tension is widely practiced because its results help to determine the indices of strength and plasticity of materials. Strength is the capability of materials to resist to plastic deformation under the action of external loads without breaking. Plasticity is the capability of materials to develop the risidual deformation without breaking. Testing in tension is the static testing under which a specimen is loaded slowly and gradually. The conditions for tension testing and the sequence to determine the results are regulated by the standard GOST 1497-84. The relation between forces and deformations are written by mechanical or electronic diagram equipment of a testing machine in the form of the curve “F~ΔL”, where F is the tensile force, L is the total elongation of a specimen. The typical tension diagrams are shown in Fig.3.
To receive specific mechanical properties of the material, which do not depend on specimen dimensions, a deformation diagram is plotted with coordinates as tension stress
where F is the tension force; A0 is the cross section area of a specimen; ΔL is the total elongation; L0 - is the gage length before the test. For the elastic range of loading, where there is a linear relation between elongation and axial force causing it (portion 0-Fpr, Fig.4), the basic characteristic is the modulus of elasticity of the material in tension or as it is often called Yound’s modulus:
Fig.4. Distinctive sectors and points of the load-extension diagram The proportional limit The elastic limit The yield (physical) point of the material The ultimate strength The point K in Fig.4 is called the breaking strength of the material. The following values characterize the ductility of a material. 1. The percentage elongation (at breaking) is determined by the relation of the length increase (of the gage length) after the fracture to the initial length:
2. The percentage reduction (at the fracture) is determined by the relation of the decrease in the cross-sectional area of the specimen to the original area of the cross-sectional area:
In the research the true ‘stress-strain’ curve is sometimes used, which is received by the replacement in the formula of the initial cross-sectional area A0 by the instantaneous value of the area. Such a curve is shown by a dashed line in Fig.4.
|

 , the elastic limit
, the elastic limit 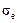 , the ultimate (tensile) strength
, the ultimate (tensile) strength  , the elongation per unit length after rupture
, the elongation per unit length after rupture  , reduction in the area of the cross-section after rupture
, reduction in the area of the cross-section after rupture  .
.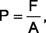
 and having the angle between the normal to it and the direction of the external force F equals
and having the angle between the normal to it and the direction of the external force F equals
 (A0 is the area of the section perpendicular to the tension axis), then
(A0 is the area of the section perpendicular to the tension axis), then
 is
is


 Fig.2. The diagram of a deformation process
Fig.2. The diagram of a deformation process
 Fig.3. The tension diagrams for different materials: (a) for the majority of metals with a gradual transition from the elastic range into the plastic one (copper, bronze, alloy steels); (b) for some metals with the spasmodic development transition into the plastic range (low-alloy steel, some bronzes); (c) for brittle materials (cast, glass, chilled and untempered steel, silumin)
Fig.3. The tension diagrams for different materials: (a) for the majority of metals with a gradual transition from the elastic range into the plastic one (copper, bronze, alloy steels); (b) for some metals with the spasmodic development transition into the plastic range (low-alloy steel, some bronzes); (c) for brittle materials (cast, glass, chilled and untempered steel, silumin)

 and normal strain
and normal strain  :
: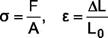


 is the minimum stress under which there is an increase in strain with no increase in stress. For many materials the risidual deformation equals 0,2% and the stress is denoted as
is the minimum stress under which there is an increase in strain with no increase in stress. For many materials the risidual deformation equals 0,2% and the stress is denoted as  .
. or tensile strength of the material is the stress corresponding to the maximum load FВ that the specimen could bear.
or tensile strength of the material is the stress corresponding to the maximum load FВ that the specimen could bear.