Связность областей и их границ
С использованием связности областей и стековой можно построить простые алгоритмы закраски как внутренней, так и гранично-определенной области. Простой алгоритм заливки. Рассмотрим простой алгоритм заливки гранично-определенной 4-х связной области (рекурсивная реализация) Заливка выполняется следующим образом: Определяется, является ли растр граничным или уже закрашенным, если нет, то растр перекрашивается, затем проверяются, и если надо перекрашиваются 4 соседних растра.
Рассмотрим итеративный алгоритм закраски 4-х связной гранично-определенной области. Логика работы алгоритма следующая: Поместить координаты затравки в стек, Пока стек не пуст.
Перекрасить растр. Для всех четырех соседних растров проверить является ли он граничным или уже перекрашен. Если нет, то занести его координаты в стек. На рисунке показан выбранный порядок перебора соседних растров, а на рис.7б соответствующий ему порядок закраски простой гранично-определенной области. Ясно, что такой алгоритм экономнее, так как в стек надо упрятывать только координаты. Рассмотренный алгоритм легко модифицировать для работы с 8-ми связными гранично-определенными областями или же для работы с внутренне-определенными. Сравнительные прогоны тестовых программ подтвердили соображения о неэкономности рекурсивного алгоритма: при стандартном окне стека в 64K с помощью рекурсивной программы можно закрасить квадратик не более чем 57×57 растров(при условии, что 1 растр = 1пикселю). Итеративная же программа при тех же условиях позволяет закрасить прямоугольник размером 110×110, истратив на массив координат 16382 байта. Как уже отмечалось, очевидный недостаток алгоритмов, непосредственно использующих связность закрашиваемой области - большие затраты памяти на стек, так как на каждый закрашенный растр в стеке по максимуму будет занесена информация о еще трех соседних. Кроме того, информация о некоторых растрах может записываться в стек многократно. Это приведет не только к перерасходу памяти, но и потере быстродействия за счет многократной раскраски одного и того же растра. Значительно более экономен далее рассмотренный построчный алгоритм заливки. Построчный алгоритм заливки с затравкой использует пространственную когерентность: растры в строке меняются только на границах; при перемещении к следующей строке размер заливаемой строки скорее всего или неизменен или меняется на 1 растр. Таким образом, на каждый закрашиваемый фрагмент строки в стеке хранятся координаты только одного начального растра, что приводит к существенному уменьшению размера стека. Последовательность работы алгоритма для гранично - определенной области следующая: Координата затравки помещается в стек, затем до исчерпания стека выполняются пункты 2-4. Координата очередной затравки извлекается из стека и выполняется максимально возможное закрашивание вправо и влево по строке с затравкой, т.е. пока не попадется граничный растр. Пусть это Хлев и Хправ, соответственно. Анализируется строка ниже закрашиваемой в пределах от Хлев до Хправ и в ней находятся крайние правые растры всех незакрашенных фрагментов. Их координаты заносятся в стек. То же самое проделывается для строки выше закрашиваемой. За счет несложной модификации служебных процедур запроса и записи строк изображения данная процедура может заливать изображение, размещенное в файле.
|

 Понятно, что несмотря на простоту и изящество программы, рекурсивная реализация проигрывает итеративной в том, что требуется много памяти для упрятывания вложенных вызовов.
Понятно, что несмотря на простоту и изящество программы, рекурсивная реализация проигрывает итеративной в том, что требуется много памяти для упрятывания вложенных вызовов.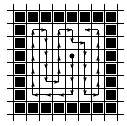 Извлечь координаты растра из стека.
Извлечь координаты растра из стека.


