Постановка задачи. На рынке предлагаются три модели машины, отличающиеся производительностью (это – стратегии) и другими параметрами.
На рынке предлагаются три модели машины, отличающиеся производительностью (это – стратегии) и другими параметрами. Предполагаем, что спрос на процессы ремонта объектов с помощью данной машины может быть пониженным (N1=25000, Цп1=50 руб./шт., Требуется выбрать оптимальную модель этой машины по заданному критерию оптимальности с использованием матрицы выигрышей или рисков.
Алгоритм решения: 1. По данным табл. 1 выбираем машину соответствующую заданному производственному участку. Пусть задана тема: «АРМ – мастера тележечного участка». Поэтому в качестве базовой машины выбираем, например, машину для обмывки тележек. 2. Сводим все параметры базовой и проектных моделей моечной машины в таблицу следующей формы «Р» – расчет:
Таблица «Р»
3. Определяем все предусмотренные в таблице параметры машин, учитывая принятые параметры стратегий и ситуаций. Расчеты выполняем с использованием электронной таблицы Excel. Функции, операторы и формулы Excel приведены в теме 2 электронного пособия и в учебном пособии [1]. С этой целью размещаем формат таблицы «Р» в ячейках электронной таблицы. Расчет параметров машины для проектных вариантов осуществляем по соотношениям (5), расчет себестоимости – по формуле (2). 4. Для всех вариантов моделей машины рассчитываем выигрыш по формуле (1). 5. Формируем в электронной таблице матрицу выигрышей по данным таблицы «Р»: Матрица выигрышей
6. Определяем итоговый выигрыш для каждой стратегии в зависимости от заданного критерия оптимальности по условиям «О». По заданному критерию выбираем оптимальную модель машины и делаем соответствующий вывод. Строим диаграмму итоговый выигрыш-модель. 7. Для критериев «минимальный средний риск», Сэвиджа строим по матрице выигрышей матрицу рисков и затем проводим процедуру оптимизации.
4.3. Алгоритм расчета и программа. Результаты расчетов. Выводы. Так как я разрабатываю АРМ мастера КРУ, а задание выбор оптимальных моделей машин для депо (ПТО), я выбрал машина для обмывки колесных пар.
Табл.1 Вариант моего задания.
Вывод: По методу минимальных средних рисков, оптимальный вариант стратегии, Вариант 1.
5. Математическое обеспечение АРМ: Моделирование производственных процессов 5.1. Модели вагоноремонтного производства
|

 0,7), средним (N2=37500, Цп2=53 руб./шт.,
0,7), средним (N2=37500, Цп2=53 руб./шт.,  0,9) и повышенным (N3=50000, Цп3=55 руб./шт.,
0,9) и повышенным (N3=50000, Цп3=55 руб./шт.,  0,6) – это ситуации, отличающиеся объемом спроса и вероятностью их появления.
0,6) – это ситуации, отличающиеся объемом спроса и вероятностью их появления. чел
чел
 шт./ч
шт./ч
 шт./ч
шт./ч
 кВт
кВт
 руб.
руб.
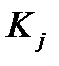

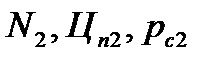


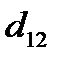

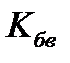

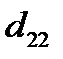


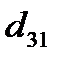


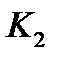
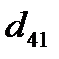


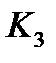
 ,*
т.руб./шт.
,*
т.руб./шт.



