Элементы теории. Алгоритм простого ранжирования заключается в следующем:
Алгоритм простого ранжирования заключается в следующем: · Цифрой 1 эксперт обозначает наиболее важный признак из предложенной их совокупности; · Цифрой 2 эксперт обозначает следующий по значимости признак и т.д.; Полученные данные сводятся в таблицу и обрабатываются методами математической статистики. По данным таблицы по каждому признаку определяют суммарный ранг:
где
Затем анализируются суммарные ранги. Признаку для которого суммарный ранг минимален присваивается высший ранг (цифра 1), а признаку у которого суммарный ранг максимален – присваивается самый низший ранг –“n” (последнее место). Точность проведенной экспертизы (степень согласованности мнений экспертов) проверяется следующим образом: · Определяют коэффициент конкордации; · Производят оценку значимости коэффициента конкордации по критерию Пирсона. Если коэффициент конкордации значим, то мнение экспертов считается согласованным, а экспертиза – достоверной. Коэффициент конкордации определяют по формуле [1]:
где
Коэффициент конкордации изменяется от 0 до 1. Если этот коэффициент равен 0, то можно считать экспертизу не достоверной, так как не существует связи между ранжировками экспертов. При значении коэффициента конкордации 1, экспертиза считается абсолютно достоверной, так как эксперты одинаково ранжируют признаки. Оценку значимости коэффициента конкордации производят по критерию Пирсона [1]:
где
Табличные значения критерия Пирсона [1]:
|

 , (3)
, (3) число экспертов;
число экспертов; ранг по
ранг по  му признаку у
му признаку у  го эксперта.
го эксперта. , (4)
, (4) ;
; ;
;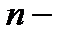 количество исследуемых признаков.
количество исследуемых признаков. . (5)
. (5) число степеней свободы;
число степеней свободы; уровень значимости.
уровень значимости.




