Применяемые виды распределения случайных величин.
Нормальное распределение. Нормальное распределение применяют тогда, когда значение случайной величины зависит от многих случайных факторов, среди которых нет доминирующих, все факторы независимы друг от друга, действие одного фактора составляет очень малую долю их совокупного действия. При этом случайные величины носят характер «случайных погрешностей» или «случайных ошибок», то есть отклонений от нормы Основные свойства нормального распределения: · Кривые распределения случайной величины по нормальному закону должны содержать одну наивысшую точку при удалении, от которой вправо и влево они непрестанно понижаются; · Все кривые симметричны относительно вертикальной прямой, проведенной через наивысшую точку; Нормальный закон двухпараметрический. Поэтому при генерации нормально распределенных случайных величин необходимо задавать (знать) среднее значение Основным нормальным законом считают закон, для которого среднее значение равно нулю, а стандартное отклонение – единице. Коэффициенты ассиметрии и эксцесса нормального распределения равны нулю. Поэтому для быстрой проверки соответствия статистических данных нормальному распределению необходимо выполнить следующие действия: Применить функцию ВЫБОРКА для выбора из всей совокупности статистических данных некоторого набора Excel. Сервис. Выборка. ОК. Входной интервал (массив расположения случайных величин). Метод выборки – случайный. Число выборок (число случайных элементов – указывается не более 30). Выходной интервал (место, куда должны быть помещены выбранные данные); Применить функцию СКОС(число1; число 2; …..n). n<=30. Эта функция возвращает коэффициент ассиметрии. Если выборка соответствует нормальному распределению, коэффициент ассиметрии должен быть равен нулю. В тех случаях, когда в выборке больших значений больше чем меньших, то это означает смещение вправо. Коэффициент ассиметрии будет больше нуля. Если в выборке преобладают меньшие значения (смещение влево), то коэффициент ассиметрии будет меньше нуля. Предельными границами отклонения случайной нормально распределенной величины являются следующие границы (правило трех сигм):
где Вероятность того, что отклонение
где
|

 .
.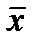 и стандартное отклонение
и стандартное отклонение  .
.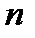 случайных элементов.
случайных элементов. , откуда
, откуда ,
, среднее квадратическое отклонение.
среднее квадратическое отклонение. по абсолютному значению случайной величины
по абсолютному значению случайной величины  не превзойдет числа
не превзойдет числа 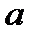
 ,
, табличное значение.
табличное значение.


