Закон сохранения импульса
Рассмотрим систему, состоящую из n материальных точек. Обозначим через
Сложим все эти уравнения
Согласно третьему закону Ньютона С учетом этого из (2) получим Введем понятие импульса системы С учетом этого из (4) находим где Если
Итак, если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не изменяется со временем. В частности, это имеет место, когда система замкнута: Импульс замкнутой системы сохраняется. Это утверждение Оказывается, в основе закона сохранения импульса лежит однородность пространства: т.е. одинаковость свойств пространства во всех его точках. Однородность пространства означает, что если замкнутую систему перенести из одного места в другое, поставив при этом все тела в ней в те же условия, в каких они находились в прежнем положении, то это не отразится на ходе всех последующих явлений.
|

 силу, с которой материальная точка k действует на i -ю материальную точку (т.е.
силу, с которой материальная точка k действует на i -ю материальную точку (т.е. 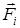 , результирующую всех внешних сил, действующих на i -тую материальную точку. Тогда, согласно второму закону Ньютона
, результирующую всех внешних сил, действующих на i -тую материальную точку. Тогда, согласно второму закону Ньютона 
 (1)
(1) (2)
(2) каждая из скобок равна нулю. Следовательно, сумма внутренних сил, действующих на тела системы всегда равна нулю, т.е.
каждая из скобок равна нулю. Следовательно, сумма внутренних сил, действующих на тела системы всегда равна нулю, т.е.  . (3)
. (3) . (4)
. (4) . (5)
. (5) , (6)
, (6) , т.е. производная по времени импульса системы равна геометрической сумме внешних сил, действующих на тела системы.
, т.е. производная по времени импульса системы равна геометрической сумме внешних сил, действующих на тела системы.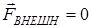 ,то соответственно
,то соответственно  и, следовательно,
и, следовательно, . (7)
. (7)


