Потенциальная энергия растянутой пружины
Обозначим через х растяжение пружины, т.е. разность длин пружины в деформированном и недеформированном состояниях. При возвращении пружины из деформированного состояния в недеформированное сила
Таким образом, потенциальная энергия упруго деформированной пружины
4.5.2. Потенциальная энергия гравитационного притяжения двух материальных точек На рис. 5 изображены две материальные точки массы m 1 и m 2. Положение их характеризуется радиусами-векторами
где R 1 и R2 – начальное и конечное расстояние между материальными точками. Эта работа равна изменению потенциальной энергии A=Wn1 -Wn2. Учитывая (14), находим, что потенциальная энергия гравитационного притяжения двух материальных точек
где R или r – расстояние между материальными точками.
|

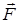 совершает работу.
совершает работу. . (12)
. (12) . (13)
. (13)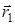 и
и  соответственно. Элементарная работа, совершаемая силами гравитационного притяжения этих точек
соответственно. Элементарная работа, совершаемая силами гравитационного притяжения этих точек  , где
, где  – сила, действующая на первую материальную точку со стороны второй, а
– сила, действующая на первую материальную точку со стороны второй, а 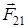 – сила, действующая на вторую
– сила, действующая на вторую  материальную точку со стороны первой; согласно 3-му закону Ньютона
материальную точку со стороны первой; согласно 3-му закону Ньютона  =-
=-  ;
; 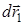 и
и  – элементарные перемещения материальных точек. С учетом этого
– элементарные перемещения материальных точек. С учетом этого  , где
, где  . Учитывая, что
. Учитывая, что 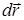 противоположно направлены и что величина
противоположно направлены и что величина  , находим
, находим  . Полная работа
. Полная работа , (14)
, (14) или
или  (15)
(15)


