Консервативные и неконсервативные силы
Сила, действующая на материальную точку, называется консервативной (потенциальной), если работа этой силы зависит только от начального и конечного положений точки. Работа консервативной силы не зависит ни от вида траектории, ни от закона движения материальной точки по траектории (см. рис. 2): Изменение направления движения точки вдоль малого участка на противоположное вызывает изменение знака элементарной работы
В этой формуле кружок на знаке интеграла показывает, что интегрирование производится по замкнутой траектории. Часто замкнутую траекторию L называют замкнутым контуром L (рис. 3). Обычно задаются направлением обхода контура L по ходу часовой стрелки. Направление элементарного вектора перемещения Следует отметить, что силы тяготения и упругости являются консервативными, а силы трения неконсервативными. В самом деле, поскольку сила трения направлена в сторону, противоположную перемещению или скорости, то работа сил трения по замкнутому пути всегда отрицательна и, следовательно, не равна нулю.
Если на материальную точку действует консервативная сила, то можно ввести скалярную функцию координат точки Потенциальную энергию определим следующим образом
где С - произвольная постоянная, а Образуем разность значений потенциальной энергии для точек 1 и 2 (см. рис. 4) и воспользуемся тем, что
Правая часть, полученного соотношения, дает работу, совершаемую на пути из точки 1
 в точку 2, проходящем через точку О; Вследствие независимости работы от формы пути такая жеработа А совершается на любом другом пути, т.е. в точку 2, проходящем через точку О; Вследствие независимости работы от формы пути такая жеработа А совершается на любом другом пути, т.е.
 . (7) . (7)
Потенциальная энергия определяется с точностью до постоянной. Однако, это не имеет существенного значения, поскольку во все физические соотношения входит либо разность значений потенциальной энергии, либо ее производная по координатам.
|

 Все силы, встречающиеся в механике, принято разделять на консервативные и неконсервативные.
Все силы, встречающиеся в механике, принято разделять на консервативные и неконсервативные. .
.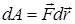 , следовательно,
, следовательно, 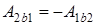 . Поэтому работа консервативной силы вдоль замкнутой траектории 1 a 2 b 1 равна нулю:
. Поэтому работа консервативной силы вдоль замкнутой траектории 1 a 2 b 1 равна нулю:  .
. Точки 1и 2, а также участки замкнутой траектории 1 a 2 и 2 b 1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю:
Точки 1и 2, а также участки замкнутой траектории 1 a 2 и 2 b 1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю: или
или  . (5)
. (5) совпадает с направлением обхода контура L. В этом случае формула (5) утверждает: циркуляция вектора
совпадает с направлением обхода контура L. В этом случае формула (5) утверждает: циркуляция вектора 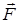 по замкнутому контуру L равна нулю.
по замкнутому контуру L равна нулю. 4.3. Потенциальная энергия
4.3. Потенциальная энергия ,называемую потенциальной энергией.
,называемую потенциальной энергией.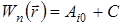 , (6)
, (6) - работа консервативной силы при перемещении материальной точки из положения
- работа консервативной силы при перемещении материальной точки из положения  вфиксированное положение
вфиксированное положение 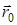 .
.
 .
.





