Кинетическая энергия
Напишем уравнение движения материальной точки (частицы) массы m, движущейся под действием сил, результирующая которых равна Умножим скалярно правую и левую часть этого равенства на элементарное перемещение точки
Так как Проинтегрировав части этого равенства вдоль траектории частицы от точки 1 до точки 2, имеем:
Согласно определению первообразной и формуле (4.3) для работы переменной силы, получим соотношение: Величина
называется кинетической энергией материальной точки. Таким образом мы приходим к формуле
из которой следует, что работа результирующей всех сил, действующих на материальную точку, расходуется на приращение кинетической энергии этой частицы. Полученный результат без труда обобщается на случай произвольной системы материальных точек. Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых эта система состоит или на которые ее можно мысленно разделить: Напишем соотношение (3) для каждой материальной точки системы, а затем все такие соотношения сложим. В результате снова получим формулу, аналогичную (3), но для системы материальных точек.
где Таким образом мы доказали теорему (4): работа всех сил, действующих на систему материальных точек, равна приращению кинетической энергии этой системы.
|
: 
.
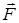, тогда
. (1)
, то легко показать, что 
Используя последнее равенство и то обстоятельство, что масса материальной точки постоянная величина, преобразуем (1) к виду 
.
.
.
(2)
, (3)
.
и 
– кинетические энергии системы, а под 
необходимо понимать сумму работ всех сил, действующих на материальные точки системы.
