Энергия, импульс в релятивистской механике
Если тело движется со скоростью v относительно инерциальной системы отсчета (ИСО) K, то помимо энергии покоя Преобразования Лоренца для энергии Е и импульса р тела имеют вид:
Если к покоящемуся телу в системе отсчета
Отсюда, Из (19), (20) следует важное соотношение между энергией Е, импульсом
Из (22) следует, что масса тела не меняется при переходе от одной ИСО к другой ИСО. В этом легко убедиться, если использовать для Е и Таким образом, в отличие от Е и Заметим, что среди элементарных частиц есть такие частицы, масса которых равна нулю, например, фотоны (кванты электромагнитного излучения, в узком смысле – частицы света), глюоны (переносчики взаимодействия между кварками), возможно, некоторые типы нейтрино. Для таких безмассовых частиц из (22) и (21) следует, что
В теории относительности, как и в ньютоновской механике, выполняются законы сохранения импульса, энергии. В теории относительности энергия и импульс аддитивны, но закон аддитивности массы не выполняется. Покажем это. Суммарная энергия Е двух свободных тел равна сумме их энергий, то есть
то есть суммарная масса зависит от угла между импульсами
|

 , оно обладает кинетической энергией
, оно обладает кинетической энергией 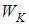 и полная энергия его
и полная энергия его  .
. ,
,  ,
,  ,
,  . (18)
. (18) применить преобразования Лоренца (18) (при этом следует учесть, что
применить преобразования Лоренца (18) (при этом следует учесть, что  ), то получается связь энергии и импульса с его скоростью:
), то получается связь энергии и импульса с его скоростью: , (19)
, (19) . (20)
. (20) . (21)
. (21) и массой т тела:
и массой т тела: . (22)
. (22) », «масса покоя т 0». Следует говорить о массе т, которая для обычных тел в теории относительности и ньютоновской механике одна и та же, что в обеих теориях масса т не зависит от системы отсчета, т.е. масса – инвариантна.
», «масса покоя т 0». Следует говорить о массе т, которая для обычных тел в теории относительности и ньютоновской механике одна и та же, что в обеих теориях масса т не зависит от системы отсчета, т.е. масса – инвариантна. . (23)
. (23) . Аналогично,
. Аналогично,  . С учетом этого из (22) находим:
. С учетом этого из (22) находим: , (24)
, (24) и
и  . Так, масса системы двух фотонов (безмассовых частиц) с энергией Е у каждого, равна
. Так, масса системы двух фотонов (безмассовых частиц) с энергией Е у каждого, равна  , если они летят в противоположные стороны и равна нулю, если они летят в одну сторону. Этот пример иллюстрирует, что в теории относительности массы не аддитивны. Следует отметить, что понимание природы массы частиц остается одной из важнейших проблем современной физики.
, если они летят в противоположные стороны и равна нулю, если они летят в одну сторону. Этот пример иллюстрирует, что в теории относительности массы не аддитивны. Следует отметить, что понимание природы массы частиц остается одной из важнейших проблем современной физики.


