Преобразования Галилея. Принцип относительности Галилея
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедлив 1- й закон Ньютона, то эти системы являются инерциальными. Галилей установил: во всех инерциальных системах отсчета законы классической механики имеют одинаковую форму. В этом заключается суть принципа относительности Галилея. Для его доказательства рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью
причем
Запишем (1) в проекциях
Формулы обратного преобразования имеют вид
Формулы (2) или (4) носят название преобразований координат Галилея. В них время считается абсолютным и поэтому не преобразуется. Соотношения (1) – (4) справедливы лишь в рамках классической механики, когда V<<c. Дифференцируя (1) по времени t, получим
где Эта формула выражает нерелятивистский закон сложения скоростей или правило сложения скоростей в классической механике (она остается справедливой и в случае, когда Дифференцируя (5) в предположении
Таким образом, ускорение в обеих инерциальных системах отсчета одно и то же, или говорят: ускорение инвариантно (неизменно, независимо) относительно преобразования Галилея. Следовательно, уравнение движения уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение носит название принципа относительности Галилея. Из него следует, что никакими механическими опытами, проведенными внутри данной системы отсчета, нельзя установить, находится ли система в покое или движется равномерно и прямолинейно.
|

 , вдоль направления OX, рис. 1.
, вдоль направления OX, рис. 1. Одну из них обозначим буквой K и будем считать неподвижной, другую, которая движется со скоростью
Одну из них обозначим буквой K и будем считать неподвижной, другую, которая движется со скоростью  . Предположим, что в начальный момент времени t= 0 начало О совпадает с
. Предположим, что в начальный момент времени t= 0 начало О совпадает с 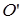 , Пусть в момент времени t движущаяся точка находится в положении М, тогда
, Пусть в момент времени t движущаяся точка находится в положении М, тогда ,
,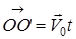 .
. . (1)
. (1)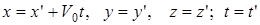 . (2)
. (2) (3)
(3)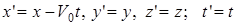 . (4)
. (4) или
или 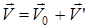 , (5)
, (5)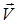 – скорость точки М в системе отсчета K, а
– скорость точки М в системе отсчета K, а  – в системе K'.
– в системе K'. , получим
, получим или
или  . (6)
. (6) не изменяется при переходе от одной инерциальной системы к другой. Таким образом:
не изменяется при переходе от одной инерциальной системы к другой. Таким образом:


