Основное уравнение релятивистской динамики
Согласно (20), релятивистский импульс Основное уравнение релятивистской динамики имеет вид
В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется. Кинетическая энергия релятивистской частицы
Согласно (19), полная энергия тела (частицы) в релятивистской механике
Из (26) следует, что при v/ c << 1 Заметим, что энергия покоящегося тела в ньютоновской механике В силу однородности времени в релятивистской механике, как и в ньютоновской механике, выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется. Заключение Итак, длительность события (времени), размеры тела не являются абсолютными величинами, а зависят от скорости тела, т. е. являются относительными. Кроме того масса и энергия оказались связанными друг с другом, хотя они являются качественно различными свойствами материи. Основной вывод теории относительности сводится к тому, что пространство и время взаимосвязаны и образуют единую форму существования материи: пространство-время. Наиболее общая теория пространства-времени называется общей теорией относительности или теорией тяготения, т.к. согласно этой теории свойства пространства-времени в данной области определяются действующими в ней полями тяготения. В изложенной выше теории действием тяготения Эйнштейн пренебрег. Поэтому она называется частной (или специальной) теорией относительности, т. к. она является частным случаем общей теории относительности, завершенной Эйнштейном позже, в 1915 г. Л Е К Ц И И № № 1 1 – 1 2. К О Л Е Б А Т Е Л Ь Н Ы Е П Р О Ц Е С С Ы В природе и технике часто происходят процессы, повторяющиеся во времени. Такие процессы называются колебаниями. Качания маятника часов, волны на воде, переменный электрический ток, свет, звук, и т.д. являются примерами колебаний различных физических величин. Все эти процессы качественно отличаются друг от друга, но оказывается, что количественные закономерности (т. е. математические выражения) этих процессов имеют много общего. Именно это обстоятельство придает учению о колебаниях его важное значение. Изучая на этих двух лекциях механические колебания, мы получим также знания - в других областях, например, из области электромагнитных колебаний, радиотехники, оптики, и др.
|

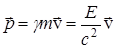 , при этом обе формулы справедливы для «тяжелых», т.е. имеющих не нулевую массу частиц. Для безмассовых частиц (т = 0)
, при этом обе формулы справедливы для «тяжелых», т.е. имеющих не нулевую массу частиц. Для безмассовых частиц (т = 0)  .
.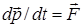 или, более подробно:
или, более подробно: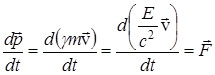 . (25)
. (25)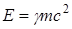 , она складывается из энергии покоя тела
, она складывается из энергии покоя тела 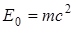 [см. (17)] и кинетической энергии
[см. (17)] и кинетической энергии 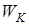 , т.е.
, т.е. 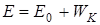 , отсюда,
, отсюда, . (26)
. (26)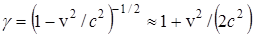 и
и  , т.е. получаем выражение кинетической энергии частицы, которое используется в ньютоновской механике.
, т.е. получаем выражение кинетической энергии частицы, которое используется в ньютоновской механике.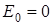 , а в релятивистской
, а в релятивистской 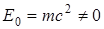 .
.


