Комплексная форма представления колебаний
Поэтому уравнение гармонического колебания (3) можно записать в экспоненциальной форме:
 .
Вещественная часть Обычно обозначение
Сложение одинаково направленных колебаний Рассмотрим сложение двух гармонических колебаний одинаковой частоты, смещения которых Используем векторную диаграмму, рис. 4; откуда следует, что
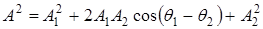
Пусть
6.1. Пусть 6.2. При (x2/A2)+(y2/B2)=1. При разных частотах складывающихся колебаний результирующие траектории будут иметь более сложный вид. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Гармонические осцилляторы
|
Согласно формуле Эйлера для комплексных чисел
, где 
.
представляет собой смещение х при гармоническом колебании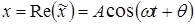 
.
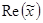опускают и пишут так
.
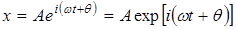и 
.
где
.
, тогда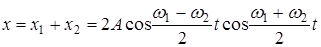
, т.е. результирующее колебание не будет гармоническим. Если колебания мало отличаются по частоте, например, 
, 
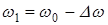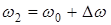, то результирующее колебание 
можно рассматривать как почти гармоническое колебание с частотой 
и медленно меняющейся амплитудой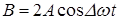 
. Такие периодические изменения амплитуды называются биениям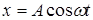и.
и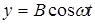 
, тогда траекторией будет прямая линия, рис. 5: 
.
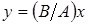, траекторией будет эллипс, (рис. 6):
