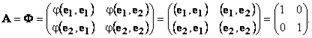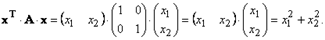Собственные числа и собственные векторы. Квадратичные формы. Матрица квадратичной формы. Привести пример.

 

Собственные числа и собственные векторы.

Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A (x), ∀ x ∈ X, y ∈ X.

Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A (x) = λ· x. Любой ненулевой вектор x ≠ 0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ.

A (x) = λ· x, x ≠ 0, x ∈ X.

Пусть A квадратная матрица. Число λ называется собственным значением матрицы A, если существует такой ненулевой вектор x, что справедливо равенство A · x = λ· x. Любой ненулевой вектор x ≠ 0, удовлетворяющий этому уравнению, называется собственным вектором матрицы A, отвечающим собственному значению λ.

A · x = λ· x, x ≠ 0.

Квадратичные формы.

Пусть числовая функция φ(x, y) — билинейная форма в пространстве L.

Числовая функция k (x) = φ(x, x) называется квадратичной формой в пространстве L.

Какова бы ни была квадратичная форма, существует единственная симметричная билинейная форма, из которой эта квадратичная форма может быть получена. Такая билинейная форма по отношению к квадратичной форме называется полярной билинейной формой. Полярная билинейная форма может быть вычислена по формуле:

Матрица квадратичной формы.

Пусть e ₁,..., e _n — базис в L. И пусть для вектора x из L задано разложение x = x ₁· e ₁+ x ₂ ·e ₂+...+ x_n · e _n. Тогда для квадратичной формы k (x) справедливо представление

Здесь φ(e_i, e_j) — значение полярной для k (x) билинейной формы φ(x, y).

Матрица A = { a_ij } называется матрицей квадратичной формы. Определённая таким образом матрица квадратичной формы является симметричной матрицей.

 

Примеры.

1) Пусть φ(x, y) = (x, y) для ∀ x∈ E, ∀y∈ E билинейная форма в пространстве E. Здесь (x, y) − скалярное произведение в пространстве E. Тогда числовая функция k (x) = φ(x, x) = (x, x) — квадратичная форма в пространстве E. Поскольку φ(x, y) = (x, y) —симметричная билинейная форма, то она является полярной билинейной формой для квадратичной формы k (x) = (x, x).

 

2) Пусть k (x) = x ₁² + x ₂² — квадратичная форма в пространстве R₂.

Пусть e ₁= (1, 0), e ₂= (0, 1) — базис в R₂. Вычислим матрицу A квадратичной формы.

Поскольку симметричная билинейная форма φ(x, y) = (x, y) — полярная для квадратичной формы k (x) = φ(x, x) то матрица A квадратичной формы совпадает с матрицей Φ; билинейной формы φ(x, y):

 

 

Проверим. Для этого подставим матрицу A в матричное представление квадратичной формы k (x)= x^T·A·x:

 

 

Матрица квадратичной формы вычислена верно.