Понятие меры.
Мера множества — неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера — это некоторая числовая функция, ставящая в соответствие каждому множеству (из некоторого семейства множеств) некоторое неотрицательное число. Кроме неотрицательности мера, как функция, должна также обладать свойством аддитивности — мера объединения непересекающихся множеств должна равняться сумме их мер. Необходимо отметить, что не всякое множество измеримо — для каждой функции меры обычно подразумевается некоторое семейство множеств (называемых измеримыми по данной мере), для которых мера существует.
Измеримые функции.
- Обычно измеримые относительно заданной меры множества составляют собственный подкласс в классе всех подмножеств пространства
 . И хотя существует несколько общих схем, позволяющих продолжать меры на большие классы измеримых множеств, иногда продолжение меры возможно лишь ценой утраты уникальных свойств исходной меры. Например, мера Лебега в конечномерных евклидовых пространствах является инвариантной относительно движений этого пространства. Всякое продолжение меры Лебега на класс всех подмножеств евклидова пространства уже не может быть инвариантным даже относительно одних только сдвигов (смотри Пример неизмеримого множества). Так что с практической точки зрения такие продолжения теряют всякую ценность.
. И хотя существует несколько общих схем, позволяющих продолжать меры на большие классы измеримых множеств, иногда продолжение меры возможно лишь ценой утраты уникальных свойств исходной меры. Например, мера Лебега в конечномерных евклидовых пространствах является инвариантной относительно движений этого пространства. Всякое продолжение меры Лебега на класс всех подмножеств евклидова пространства уже не может быть инвариантным даже относительно одних только сдвигов (смотри Пример неизмеримого множества). Так что с практической точки зрения такие продолжения теряют всякую ценность.
- На прямой и двумерной плоскости существует бесконечное число расширений лебеговой меры с Борелевской
 -алгебры, на множество всех ограниченных подмножеств, сохраняющее конечную аддитивность меры и такую, что конгруэнтные множества имеют равную меру. Начиная с размерности 3, это сделать невозможно.
-алгебры, на множество всех ограниченных подмножеств, сохраняющее конечную аддитивность меры и такую, что конгруэнтные множества имеют равную меру. Начиная с размерности 3, это сделать невозможно.
Мера Лебега. Внешняя мера.
Для произвольного подмножества  числовой прямой можно найти сколь угодно много различных систем из конечного или счётного числа интервалов, объединение которых содержит множество
числовой прямой можно найти сколь угодно много различных систем из конечного или счётного числа интервалов, объединение которых содержит множество  . Назовём такие системы покрытиями. Так как сумма длин интервалов, составляющих любое покрытие, есть величина неотрицательная, она ограничена снизу, и, значит, множество длин всех покрытий имеет точную нижнюю грань. Эта грань, зависящая только от множества
. Назовём такие системы покрытиями. Так как сумма длин интервалов, составляющих любое покрытие, есть величина неотрицательная, она ограничена снизу, и, значит, множество длин всех покрытий имеет точную нижнюю грань. Эта грань, зависящая только от множества  , и называется внешней мерой:
, и называется внешней мерой:
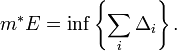
Варианты обозначения внешней меры:
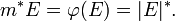
Внешняя мера любого интервала совпадает с его длиной, что является следствием счетной аддитивности меры Лебега на полукольце интервалов, отрезков и полуинтервалов. Если точнее, то указанная счетная аддитивность дает  , тогда как противоположное неравенство действительно очевидно и напрямую вытекает из определения внешней меры. Более того, можно привести такой пример меры на алгебре, что внешняя мера некоторого множества из этой алгебры строго меньше его исходной меры. Подробнее можно почитать в книге Богачева и Смолянова (Действительный и функциональный анализ...).
, тогда как противоположное неравенство действительно очевидно и напрямую вытекает из определения внешней меры. Более того, можно привести такой пример меры на алгебре, что внешняя мера некоторого множества из этой алгебры строго меньше его исходной меры. Подробнее можно почитать в книге Богачева и Смолянова (Действительный и функциональный анализ...).
Свойства внешней меры
-

-

-
 , где
, где  — открытое множество. Действительно, достаточно в качестве
— открытое множество. Действительно, достаточно в качестве  взять сумму интервалов, составляющих покрытие
взять сумму интервалов, составляющих покрытие  , такую что
, такую что  . Существование такого покрытия следует из определения точной нижней грани.
. Существование такого покрытия следует из определения точной нижней грани.
Внутренняя мера
Если множество  ограничено, то внутренней мерой множества
ограничено, то внутренней мерой множества  называется разность между длиной сегмента
называется разность между длиной сегмента  содержащего
содержащего  и внешней мерой дополнения
и внешней мерой дополнения  в
в  :
:
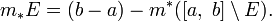
Для неограниченных множеств,  определяется как точная верхняя грань
определяется как точная верхняя грань  по всем отрезкам
по всем отрезкам  .
.
Измеримые множества
Множество называется измеримым по Лебегу, если его внешняя и внутренняя меры равны. Тогда общее значение последних называется мерой множества по Лебегу и обозначается  ,
,  или
или  .
.
Пример неизмеримого множества
Пример неизмеримого по Лебегу множества построил Дж. Витали в 1905 году. Рассмотрим следующее отношение эквивалентности  на отрезке
на отрезке  :
:  если разница
если разница  рациональна. Далее, из каждого класса эквивалентности выберем по представителю — одной точке (здесь мы пользуемся аксиомой выбора). Тогда полученное множество
рациональна. Далее, из каждого класса эквивалентности выберем по представителю — одной точке (здесь мы пользуемся аксиомой выбора). Тогда полученное множество  представителей будет неизмеримым.
представителей будет неизмеримым.
Действительно, если сдвинуть  счётное число раз на все рациональные числа в интервале
счётное число раз на все рациональные числа в интервале  , то объединение будет содержать весь отрезок
, то объединение будет содержать весь отрезок  но при этом оно будет содержаться в отрезке
но при этом оно будет содержаться в отрезке  . При этом «сдвинутые копии» множества
. При этом «сдвинутые копии» множества  не будут пересекаться друг с другом, что непосредственно следует из построения
не будут пересекаться друг с другом, что непосредственно следует из построения  и
и  .
.
Предположим, что  измеримо — тогда, в силу счётной аддитивности меры Лебега, получаем, что
измеримо — тогда, в силу счётной аддитивности меры Лебега, получаем, что  и
и  — противоречие.
— противоречие.
Интеграл Лебега.
Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций. Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах.
Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.
Определение интеграла Лебега.
Интеграл Лебега определяют пошагово, переходя от более простых функций к сложным. Будем считать, что дано пространство с мерой  , и на нем определена борелевская функция
, и на нем определена борелевская функция  .
.
Определение 1. Пусть  — индикатор некоторого измеримого множества, то есть
— индикатор некоторого измеримого множества, то есть  , где
, где  . Тогда интеграл Лебега функции
. Тогда интеграл Лебега функции  по определению:
по определению:
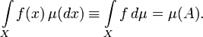
Определение 2. Пусть  — простая функция, то есть
— простая функция, то есть  , где
, где  , а
, а  — конечное разбиение
— конечное разбиение  на измеримые множества. Тогда
на измеримые множества. Тогда
 .
.
Определение 3. Пусть теперь  — неотрицательная функция, то есть
— неотрицательная функция, то есть  . Рассмотрим все простые функции
. Рассмотрим все простые функции  , такие что
, такие что  . Обозначим это семейство
. Обозначим это семейство  . Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от
. Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от  задаётся формулой:
задаётся формулой:
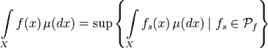
Наконец, если функция  произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:
произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:
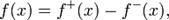
где
 .
.
Определение 4. Пусть  — произвольная измеримая функция. Тогда ее интеграл задаётся формулой:
— произвольная измеримая функция. Тогда ее интеграл задаётся формулой:
 .
.
Определение 5. Пусть наконец  произвольное измеримое множество. Тогда по определению
произвольное измеримое множество. Тогда по определению
 ,
,
где  — индикатор-функция множества
— индикатор-функция множества  .
.

 . И хотя существует несколько общих схем, позволяющих продолжать меры на большие классы измеримых множеств, иногда продолжение меры возможно лишь ценой утраты уникальных свойств исходной меры. Например, мера Лебега в конечномерных евклидовых пространствах является инвариантной относительно движений этого пространства. Всякое продолжение меры Лебега на класс всех подмножеств евклидова пространства уже не может быть инвариантным даже относительно одних только сдвигов (смотри Пример неизмеримого множества). Так что с практической точки зрения такие продолжения теряют всякую ценность.
. И хотя существует несколько общих схем, позволяющих продолжать меры на большие классы измеримых множеств, иногда продолжение меры возможно лишь ценой утраты уникальных свойств исходной меры. Например, мера Лебега в конечномерных евклидовых пространствах является инвариантной относительно движений этого пространства. Всякое продолжение меры Лебега на класс всех подмножеств евклидова пространства уже не может быть инвариантным даже относительно одних только сдвигов (смотри Пример неизмеримого множества). Так что с практической точки зрения такие продолжения теряют всякую ценность. -алгебры, на множество всех ограниченных подмножеств, сохраняющее конечную аддитивность меры и такую, что конгруэнтные множества имеют равную меру. Начиная с размерности 3, это сделать невозможно.
-алгебры, на множество всех ограниченных подмножеств, сохраняющее конечную аддитивность меры и такую, что конгруэнтные множества имеют равную меру. Начиная с размерности 3, это сделать невозможно. числовой прямой можно найти сколь угодно много различных систем из конечного или счётного числа интервалов, объединение которых содержит множество
числовой прямой можно найти сколь угодно много различных систем из конечного или счётного числа интервалов, объединение которых содержит множество 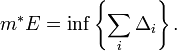
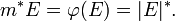
 , тогда как противоположное неравенство действительно очевидно и напрямую вытекает из определения внешней меры. Более того, можно привести такой пример меры на алгебре, что внешняя мера некоторого множества из этой алгебры строго меньше его исходной меры. Подробнее можно почитать в книге Богачева и Смолянова (Действительный и функциональный анализ...).
, тогда как противоположное неравенство действительно очевидно и напрямую вытекает из определения внешней меры. Более того, можно привести такой пример меры на алгебре, что внешняя мера некоторого множества из этой алгебры строго меньше его исходной меры. Подробнее можно почитать в книге Богачева и Смолянова (Действительный и функциональный анализ...).

 , где
, где  — открытое множество. Действительно, достаточно в качестве
— открытое множество. Действительно, достаточно в качестве  . Существование такого покрытия следует из определения точной нижней грани.
. Существование такого покрытия следует из определения точной нижней грани. содержащего
содержащего 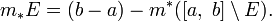
 определяется как точная верхняя грань
определяется как точная верхняя грань  по всем отрезкам
по всем отрезкам  ,
,  или
или  .
. на отрезке
на отрезке  :
:  если разница
если разница  рациональна. Далее, из каждого класса эквивалентности выберем по представителю — одной точке (здесь мы пользуемся аксиомой выбора). Тогда полученное множество
рациональна. Далее, из каждого класса эквивалентности выберем по представителю — одной точке (здесь мы пользуемся аксиомой выбора). Тогда полученное множество  , то объединение будет содержать весь отрезок
, то объединение будет содержать весь отрезок  но при этом оно будет содержаться в отрезке
но при этом оно будет содержаться в отрезке  . При этом «сдвинутые копии» множества
. При этом «сдвинутые копии» множества  и
и  — противоречие.
— противоречие. , и на нем определена борелевская функция
, и на нем определена борелевская функция  .
. — индикатор некоторого измеримого множества, то есть
— индикатор некоторого измеримого множества, то есть  , где
, где  . Тогда интеграл Лебега функции
. Тогда интеграл Лебега функции 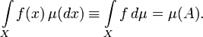
 — простая функция, то есть
— простая функция, то есть  , где
, где  , а
, а  — конечное разбиение
— конечное разбиение  .
. — неотрицательная функция, то есть
— неотрицательная функция, то есть  . Рассмотрим все простые функции
. Рассмотрим все простые функции  , такие что
, такие что  . Обозначим это семейство
. Обозначим это семейство  . Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от
. Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от  задаётся формулой:
задаётся формулой: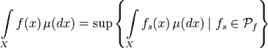
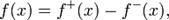
 .
. .
. ,
, — индикатор-функция множества
— индикатор-функция множества  .
.


