Метрические пространства. Метрика. Примеры. Сжатые отображения.
Метрическое пространство.
Метри́ческим простра́нством называется множество, в котором определено расстояние между любой парой элементов. Метрическое пространство есть пара
Прим.: Из аксиом следует неотрицательность функции расстояния, поскольку Сжатые отображения. Сжатые отображения одно из основных положений теории метрических пространств о существовании и единственности неподвижной точки множества при некотором специальном («сжимающем») отображении его в себя. С. о. п. применяют главным образом в теории дифференциальных и интегральных уравнений. Произвольное отображение А метрического пространства М в себя, которое каждой точке х из М сопоставляет некоторую точку у = Ax из М, порождает в пространстве М уравнение Ax = х. (*) Действие отображения А на точку х можно интерпретировать как перемещение её в точку у = Ax. Точка х называется неподвижной точкой отображения А, если выполняется равенство (*). Т. о. вопрос о разрешимости уравнения (*) является вопросом о нахождении неподвижных точек отображения А. Отображение А метрического пространства М в себя называется сжатым, если существует такое положительное число a < 1, что для любых точек х и у из М выполняется неравенство d (Ax, Ау) £ a d (х, у), где символ d (u, u) означает расстояние между точками u и u метрического пространства М. С. о. п. утверждает, что каждое сжатое отображение полного метрического пространства в себя имеет, и притом только одну, неподвижную точку. Кроме того, для любой начальной точки x0 из М последовательность { xn }, определяемая рекуррентными соотношениями xn = Axn-1, n = 1,2,..., имеет своим пределом неподвижную точку х отображения А. При этом справедлива следующая оценка погрешности:
С. о. п. позволяет единым методом доказывать важные теоремы о существовании и единственности решений дифференциальных, интегральных и др. уравнений. В условиях применимости С. о. п. решение может быть с наперёд заданной точностью вычислено последовательных приближений методом. С помощью определённого выбора полного метрического пространства М и построения отображения А эти задачи сводят предварительно к уравнению (*), а затем находят условия, при которых отображение А оказывается сжатым. Примеры.
Сходимость отображений по этой метрике равнозначна их равномерной сходимости на всём пространстве В частном случае, когда
Для того, чтобы эта функция стала метрикой, в первых двух пространствах необходимо отождествить функции, отличающиеся на множестве меры 0. В противном случае эта функция будет всего лишь полуметрикой. (В пространстве функций, непрерывных на отрезке, функции, отличающиеся на множестве меры 0, и так совпадают.)
где
|

 , где
, где  — множество (подлежащее множество метрического пространства, множество точек метрического пространства), а
— множество (подлежащее множество метрического пространства, множество точек метрического пространства), а  — числовая функция (метрика пространства), которая определена на декартовом произведении
— числовая функция (метрика пространства), которая определена на декартовом произведении  и принимает значения в множестве вещественных чисел — такая, что для точек
и принимает значения в множестве вещественных чисел — такая, что для точек 
 (аксиома тождества).
(аксиома тождества). (аксиома симметрии).
(аксиома симметрии). (аксиома треугольника или неравенство треугольника).
(аксиома треугольника или неравенство треугольника).
 .
. , если
, если  , и
, и  во всех остальных случаях.
во всех остальных случаях. и евклидово пространство являются полными метрическими пространствами.
и евклидово пространство являются полными метрическими пространствами. — пространство непрерывных и ограниченных отображений из топологического пространства
— пространство непрерывных и ограниченных отображений из топологического пространства  . Расстояние между двумя отображениями
. Расстояние между двумя отображениями  и
и  из этого пространства определяется как
из этого пространства определяется как 
 всех непрерывных функций на пространстве X с метрикой равномерной сходимости.
всех непрерывных функций на пространстве X с метрикой равномерной сходимости.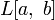 ,
, 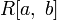 ,
,  — пространства функций на отрезке
— пространства функций на отрезке  , соответственно интегрируемых по Лебегу, интегрируемых по Риману, и непрерывных. В них расстояние можно определить по формуле:
, соответственно интегрируемых по Лебегу, интегрируемых по Риману, и непрерывных. В них расстояние можно определить по формуле: 
 метрика вводится по формуле:
метрика вводится по формуле: 
 — метрика равномерной сходимости на
— метрика равномерной сходимости на 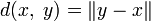 .
.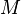 можно превратить в метрическое пространство, определив расстояние как точную нижнюю грань длин путей, соединяющих пару точек.
можно превратить в метрическое пространство, определив расстояние как точную нижнюю грань длин путей, соединяющих пару точек. можно превратить в метрическое пространство, определив расстояние как минимальное число рёбер в пути, соединяющем вершины. Более общо: если каждому рёбру графа приписать положительное число (длину ребра), расстояние между вершинами можно определить как минимальную сумму длин рёбер вдоль любых путей из одной вершины в другую.
можно превратить в метрическое пространство, определив расстояние как минимальное число рёбер в пути, соединяющем вершины. Более общо: если каждому рёбру графа приписать положительное число (длину ребра), расстояние между вершинами можно определить как минимальную сумму длин рёбер вдоль любых путей из одной вершины в другую. любого метрического пространства
любого метрического пространства 



