Функционалы. Функциональные пространства.
Функционал.
Функциона́л — это отображение, заданное на произвольном множестве и имеющее числовую область значений: обычно множество вещественных чисел Область определения функционала может быть любым множеством. Если область определения является топологическим пространством, можно определить непрерывный функционал; если область определения является линейным пространством над Функционал, заданный на топологическом пространстве Функционал, заданный на топологическом пространстве В более широком смысле функционалом называется любое отображение из произвольного множества в произвольное (не обязательно числовое) кольцо. Функционал, заданный на линейном пространстве, и сохраняющий сложение и умножение на константу, называется линейным функционалом. (Отображение линейного пространства в линейное пространство называют оператором). Пожалуй, самый простой функционал — проекция - (сопоставление вектору одной из его координат). Довольно часто в роли линейного пространства выступает то или иное пространство функций (непрерывные функции на отрезке, интегрируемые функции на плоскости и т. д.). Поэтому в прикладных областях под функционалом часто понимают функцию от функций, отображение, переводящее функцию в число (действительное или комплексное). Функционал на линейном пространстве называется положительно определённым, если его значение неотрицательно и равно нулю только в нуле. Отображение, переводящее вектор в его норму, является выпуклым положительно определённым функционалом, это один из самых распространённых функционалов. В физике часто используется действие — тоже функционал. Задачи оптимизации формулируются на языке функционалов: найти решение (уравнения, системы уравнений, системы ограничений, системы неравенств, системы включений и т. п.), доставляющее экстремум (минимум или максимум) заданному функционалу. Функционалы также рассматриваются в вариационном анализе. Функционал в линейном пространстве Позднее от понятия традиционного функционала отделилось понятие функционала в линейном пространстве, как функции, отображающей элементы линейного пространства в его пространство скаляров. Зачастую (например, когда пространство функций является линейным пространством) эти две разновидности понятия «функционал» совпадают, в то же время они не тождественны и не поглощают друг друга. Особенно важной разновидностью функционалов являются линейные функционалы. Линейные функционалы. Линейный функционал — функционал, обладающий свойством линейности по своему аргументу:
где Иными словами, это линейное отображение из (некоторого) пространства функций во множество чисел — чаще всего подразумеваемых вещественными, или, еще иначе, линейный оператор, действующий из (некоторого) пространства функций в Линейные функционалы играют особую роль в функциональном анализе.
(может быть также использовано интегрирование с весовой функцией).
|

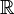 или комплексных чисел
или комплексных чисел 
 , называется непрерывным, если он непрерывен как отображение в топологическое пространство
, называется непрерывным, если он непрерывен как отображение в топологическое пространство  , если он непрерывен в этой точке как отображение в топологическое пространство
, если он непрерывен в этой точке как отображение в топологическое пространство 
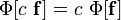
 — линейный функционал,
— линейный функционал,  и
и  — функции из его области определения,
— функции из его области определения,  — число (константа).
— число (константа).



