Ортогональный и ортонормированный базис. Процесс ортогонализации. Сопряженные векторы в евклидовом пространстве.
Ортогональный базис.
Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты. Ортогональный базис — базис, составленный из попарно ортогональных векторов.
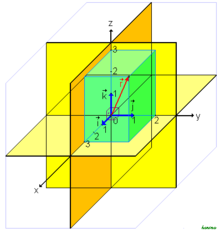
Ортонормированный базис в 3-мерном евклидовом пространстве Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами. Последнее удобно записывается при помощи символа Кронекера:
то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности. Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы). Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически. Коэффициенты в разложении вектора по ортогональному базису:
можно найти так:
Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора
Ортонормированный базис. Ортонормированная система, состоящая из n векторов n -мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом. Если e 1, e 2, ..., e n — ортонормированный базис n -мерного евклидова пространства и x = x 1 e1 + x 2 e2 +... + xn e n — разложение вектора x по этому базису, то координаты x i вектора x в ортонормированном базисе вычисляются по формулам x i =(x, e i), i = 1, 2,..., n. В любом конечномерном евклидовом пространстве существует ортонормированный базис. Любую ортонормированную систему векторов конечномерного евклидова пространства можно дополнить до ортонормированного базиса. Процесс Грама ― Шмидта
Процесс Грама (англ.) ― Шмидта — это один из алгоритмов, в которых на основе счётного множества линейно независимых векторов Определим оператор проекции следующим образом:
где Классический процесс Грама — Шмидта выполняется следующим образом:
На основе каждого вектора Результаты процесса Грама — Шмидта:
Вычисление ой комбинацией векторов
|



 ), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
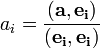 .
.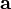 квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:
квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису: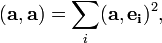
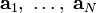 строится множество ортогональных векторов
строится множество ортогональных векторов 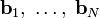 или ортонормированных векторов
или ортонормированных векторов 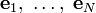 , причём так, что каждый вектор
, причём так, что каждый вектор 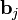 или
или 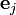 может быть выражен линейн Пусть имеются линейно независимые векторы
может быть выражен линейн Пусть имеются линейно независимые векторы 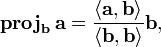
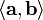 — скалярное произведение векторов
— скалярное произведение векторов 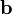 . Этот оператор проецирует вектор
. Этот оператор проецирует вектор 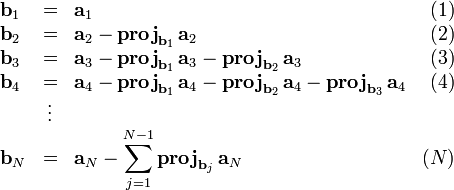
 может быть получен нормированный вектор:
может быть получен нормированный вектор: 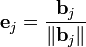 (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).
(у нормированного вектора направление будет таким же, как у исходного, а длина — единичной). .
.


