Нормированные пространства. Норма. Примеры.
Нормированное пространство. В трёхмерном пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:
Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством. Определение. Полунормированным векторным пространством называется пара Нормированным векторным пространством называется пара Часто обозначение
Топологическая структура. Для любого полунормированного векторного пространства мы можем задать расстояние между двумя векторами Особый интерес представляют полные нормированные пространства, называемые банаховыми пространствами. Любое нормированное векторное пространство Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, так как они порождают одну и ту же топологию. А так как любое евклидово пространство полно, мы можем сделать вывод, что все конечномерные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство Топология полунормированного вектора обладает несколькими интересными свойствами. Взяв окрестностную систему
с помощью
Более того, существует базис окрестностей для Линейные отображения и двойственные пространства. Наиболее важными отображениями между двумя нормированными векторными пространствами являются непрерывные линейные отображения. Нормированные векторные пространства с такими отображениями образуют категорию. Норма — это непрерывная функция в своём векторном пространстве. Все линейные отображения между конечномерными векторными пространствами также непрерывны. Изометрией между двумя нормированными векторными пространствами называется линейное отображение Говоря о нормированных векторных пространствах мы должны упомянуть двойственные пространства. Двойственное пространство
Введение такой нормы превращает Нормированные пространства как фактор-пространства полунормированных пространств. Определения многих нормированных пространств (например, банахова пространства) включают в себя полунорму, определённую в векторном пространстве, а затем нормированное пространство определяется как факторпространство с помощью подпространства элементов, чья полунорма равна нулю. Например, в случае пространств Lp, функция, определяемая как
является полунормой в векторном пространстве всех функций, интеграл Лебега от которых (справа) определён и конечен. Однако полунорма равна нулю для всех функций, носитель которых имеет нулевую меру Лебега. Эти функции образуют подпространство, которое мы «вычёркиваем», делая их эквивалентными нулевой функции. Конечные произведения пространств. Для данных
с векторным сложением, определённым как
и скалярным умножением, определённым как
Определим новую функцию
как
которая будет полунормой в
|

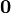 , равна нулю; длина любого другого вектора положительна.
, равна нулю; длина любого другого вектора положительна. , где
, где  — векторное пространство, а
— векторное пространство, а  — полунорма в
— полунорма в 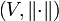 , где
, где 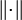 — норма в
— норма в  и
и  как
как  . Такое полунормированное пространство с определённым таким образом расстоянием называется полунормированным метрическим пространством, в котором мы можем определить такие понятия как непрерывность и сходимость. Более абстрактно, любое полунормированное векторное пространство является топологическим векторным пространством и, таким образом, несёт топологическую структуру, порождённую полунормой.
. Такое полунормированное пространство с определённым таким образом расстоянием называется полунормированным метрическим пространством, в котором мы можем определить такие понятия как непрерывность и сходимость. Более абстрактно, любое полунормированное векторное пространство является топологическим векторным пространством и, таким образом, несёт топологическую структуру, порождённую полунормой. компактен, что может быть тогда и только тогда, когда
компактен, что может быть тогда и только тогда, когда 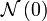 около
около  , мы можем построить все остальные окрестностные системы как
, мы можем построить все остальные окрестностные системы как

 , сохраняющее норму (то есть
, сохраняющее норму (то есть  для всех векторов
для всех векторов  называется изометрическим изоморфизмом. Изометрически изоморфные нормированные векторные пространства можно считать равноправными для практически любых целей.
называется изометрическим изоморфизмом. Изометрически изоморфные нормированные векторные пространства можно считать равноправными для практически любых целей. нормированного векторного пространства
нормированного векторного пространства 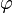 определяется как
определяется как

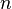 полунормированных пространств
полунормированных пространств 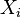 с полунормами
с полунормами 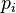 мы можем определить произведение пространств как
мы можем определить произведение пространств как




 . Функция
. Функция 


