Линейные пространства. Аксиомы. Определение поля.
Линейные пространства. Линейным (векторным) пространством называется множество 1) 2) 3) существует такой элемент 4) для каждого вектора 5) 6) 7) 8)
Условия 1-8 называются аксиомами линейного пространства. Знак равенства, поставленный между векторами, означает, что в левой и правой частях равенства представлен один и тот же элемент множества В определении линейного пространства операция умножения вектора на число введена для действительных чисел. Такое пространство называют линейным пространством над полем действительных (вещественных) чисел, или, короче, вещественным линейным пространством. Если в определении вместо поля Замечания: 1) Аксиомы 1-4 показывают, что линейное пространство является коммутативной группой относительно операции сложения. 2) Аксиомы 5 и 6 определяют дистрибутивность операции умножения вектора на число по отношению к операции сложения векторов (аксиома 5) или к операции сложения чисел (аксиома 6). Аксиома 7, иногда называемая законом ассоциативности умножения на число, выражает связь двух разных операций: умножения вектора на число и умножения чисел. Свойство, определяемое аксиомой 8, называется унитарностью операции умножения вектора на число. 3) Линейное пространство — это непустое множество, так как обязательно содержит нулевой вектор. 4) Операции сложения векторов и умножения вектора на число называются линейными операциями над векторами. 5) Разностью векторов 6) Два ненулевых вектора
Следствия аксиом линейного пространства.
1) В линейном пространстве существует единственный нулевой вектор. 2) В линейном пространстве для любого вектора 3) Произведение произвольного вектора пространства на число нуль равно нулевому вектору, т.е. 4) Произведение нулевого вектора на любое число равно нулевому вектору, т.е 5) Вектор, противоположный данному вектору, равен произведению данного вектора на число (-1), т.е. 6) В выражениях вида Докажем, например, первые два свойства. Единственность нулевого вектора. Если
Остальные свойства доказываются аналогично.
|

 произвольных элементов, называемых векторами, в котором определены операции сложения векторов и умножения вектора на число, т.е. любым двум векторам
произвольных элементов, называемых векторами, в котором определены операции сложения векторов и умножения вектора на число, т.е. любым двум векторам  и
и  поставлен в соответствие вектор
поставлен в соответствие вектор 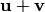 , называемый суммой векторов
, называемый суммой векторов  из поля действительных чисел
из поля действительных чисел  поставлен в соответствие вектор
поставлен в соответствие вектор 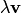 , называемый произведением вектора
, называемый произведением вектора 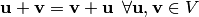 (коммутативность сложения);
(коммутативность сложения); (ассоциативность сложения);
(ассоциативность сложения); , называемый нулевым вектором, что
, называемый нулевым вектором, что  ;
; , называемый противоположным вектору
, называемый противоположным вектору  ;
;


 .
.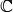 , то получим линейное пространство над полем комплексных чисел, или, короче, комплексное линейное пространство. В качестве числового поля можно выбрать и поле
, то получим линейное пространство над полем комплексных чисел, или, короче, комплексное линейное пространство. В качестве числового поля можно выбрать и поле  рациональных чисел, при этом получим линейное пространство над полем рациональных чисел. Далее, если не оговорено противное, будут рассматриваться вещественные линейные пространства. В некоторых случаях для краткости будем говорить о пространстве, опуская слово линейное, так как все пространства, рассматриваемые ниже — линейные.
рациональных чисел, при этом получим линейное пространство над полем рациональных чисел. Далее, если не оговорено противное, будут рассматриваться вещественные линейные пространства. В некоторых случаях для краткости будем говорить о пространстве, опуская слово линейное, так как все пространства, рассматриваемые ниже — линейные. и
и  называется сумма вектора
называется сумма вектора  с противоположным вектором
с противоположным вектором  и обозначается:
и обозначается:  .
. и
и  , что
, что  . Понятие коллинеарности распространяется на любое конечное число векторов. Нулевой вектор
. Понятие коллинеарности распространяется на любое конечное число векторов. Нулевой вектор  считается коллинеарным с любым вектором.
считается коллинеарным с любым вектором. существует единственный противоположный вектор
существует единственный противоположный вектор  .
. для любого числа
для любого числа  .
. (сумма конечного числа векторов) или
(сумма конечного числа векторов) или  (произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать.
(произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать. и
и  — два нулевых вектора, то по аксиоме 3 получаем два равенства:
— два нулевых вектора, то по аксиоме 3 получаем два равенства:  или
или  , левые части которых равны по аксиоме 1. Следовательно, равны и правые части, т.е.
, левые части которых равны по аксиоме 1. Следовательно, равны и правые части, т.е.  . Единственность противоположного вектора. Если вектор
. Единственность противоположного вектора. Если вектор 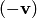 и
и 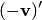 , то по аксиомам 2, 3,4 получаем их равенство:
, то по аксиомам 2, 3,4 получаем их равенство:



