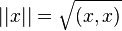Банахово пространство.
Ба́нахово пространство — нормированное векторное пространство, полное по метрике, порождённой нормой. Основной объект изучения функционального анализа. Названо по имени польского математика Стефана Банаха.
Примеры.
Далее через  обозначено одно из полей
обозначено одно из полей 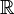 или
или  .
.
- Евклидовы пространства
 с евклидовой нормой, определяемой для
с евклидовой нормой, определяемой для 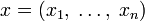 как
как  , являются банаховыми пространствами.
, являются банаховыми пространствами. - Пространство всех непрерывных функций
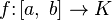 , определённых на закрытом интервале
, определённых на закрытом интервале  будет банаховым пространством, если мы определим его норму как
будет банаховым пространством, если мы определим его норму как  . Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как
. Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как  . Этот пример можно обобщить к пространству
. Этот пример можно обобщить к пространству  всех непрерывных функций
всех непрерывных функций  , где
, где  — компактное пространство, или к пространству всех ограниченных непрерывных функций
— компактное пространство, или к пространству всех ограниченных непрерывных функций  , где
, где  — любое топологическое пространство, или даже к пространству
— любое топологическое пространство, или даже к пространству  всех ограниченных функций
всех ограниченных функций  , где
, где  — любое множество. Во всех этих примерах мы можем перемножать функции, оставаясь в том же самом пространстве: все эти примеры являются банаховыми алгебрами.
— любое множество. Во всех этих примерах мы можем перемножать функции, оставаясь в том же самом пространстве: все эти примеры являются банаховыми алгебрами. - Если
 — вещественное число, то пространство всех бесконечных последовательностей
— вещественное число, то пространство всех бесконечных последовательностей  элементов из
элементов из  , таких что ряд
, таких что ряд  сходится, является банаховым относительно нормы, равной корню степени
сходится, является банаховым относительно нормы, равной корню степени  из суммы этого ряда, и обозначается
из суммы этого ряда, и обозначается  .
. - Банахово пространство
 состоит из всех ограниченных последовательностей элементов из
состоит из всех ограниченных последовательностей элементов из  ; норма такой последовательности определяется как точная верхняя грань абсолютных величин (модулей) элементов последовательности.
; норма такой последовательности определяется как точная верхняя грань абсолютных величин (модулей) элементов последовательности. - Снова, если
 — вещественное число, можно рассматривать все функции интегрируемыми по Лебегу. Корень степени
— вещественное число, можно рассматривать все функции интегрируемыми по Лебегу. Корень степени  этого интеграла определим как норму
этого интеграла определим как норму  . Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом:
. Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом:  и
и 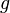 эквивалентны тогда и только тогда, когда норма
эквивалентны тогда и только тогда, когда норма  равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как
равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как  . Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например,
. Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например, 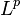 -пространства.
-пространства. - Если
 и
и  — банаховы пространства, то можно составить их прямую сумму
— банаховы пространства, то можно составить их прямую сумму  , которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств.
, которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств. - Если
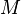 — замкнутое подпространство банахова пространства
— замкнутое подпространство банахова пространства  , то факторпространство
, то факторпространство  снова является банаховым.
снова является банаховым. - Любое гильбертово пространство тоже является банаховым. Обратное неверно.
- Если
 и
и  — банаховы пространства над одним полем
— банаховы пространства над одним полем  , тогда множество непрерывных
, тогда множество непрерывных  -линейных отображений
-линейных отображений  обозначается
обозначается 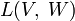 . Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными.
. Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными. 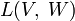 — векторное пространство, и, если норма задана как
— векторное пространство, и, если норма задана как 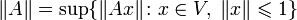 , является также и банаховым.
, является также и банаховым. - Пространство
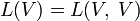 представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений.
представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений.
Гильбертово пространство.
Ги́льбертово простра́нство — обобщение евклидова пространства, допускающее бесконечную размерность. Названо в честь Давида Гильберта.
Важнейшим объектом исследования в гильбертовом пространстве являются линейные операторы. Само понятие гильбертова пространства сформировалось в работах Д. Гильберта и Э. Шмидта по теории интегральных уравнений, а абстрактное определение было дано в работах Дж. Неймана, Ф. Рисса и М. Стоуна по теории эрмитовых операторов.
Гильбертово пространство - линейное (векторное) пространство (над полем вещественных или комплексных чисел), в котором для любых двух элементов пространства  и
и 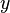 определено скалярное произведение
определено скалярное произведение  и полное относительно порожденной скалярным произведением метрики
и полное относительно порожденной скалярным произведением метрики  . Если условие полноты пространства не выполнено, то говорят о предгильбертовомпространстве. Однако, большинство из известных (используемых) пространств либо являются полными, либо могут быть пополнены.
. Если условие полноты пространства не выполнено, то говорят о предгильбертовомпространстве. Однако, большинство из известных (используемых) пространств либо являются полными, либо могут быть пополнены.
Таким образом, гильбертово пространство есть банахово пространство (полное нормированное пространство), норма которого порождена положительно определённым скалярным произведением и определяется как 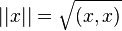
Норма в произвольном нормированном пространстве может порождаться некоторым скалярным произведением тогда и только тогда, когда выполнено следующее равенство (тождество) параллелограмма:

Если удовлетворяющее тождеству параллелограмма банахово пространство является вещественным, то отвечающее его норме скалярное произведение задаётся равенством

Если это пространство является комплексным, то отвечающее его норме скалярное произведение задаётся равенством

(поляризационное тождество).

 обозначено одно из полей
обозначено одно из полей 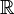 или
или  .
. с евклидовой нормой, определяемой для
с евклидовой нормой, определяемой для 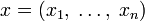 как
как  , являются банаховыми пространствами.
, являются банаховыми пространствами.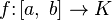 , определённых на закрытом интервале
, определённых на закрытом интервале  будет банаховым пространством, если мы определим его норму как
будет банаховым пространством, если мы определим его норму как  . Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как
. Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как  . Этот пример можно обобщить к пространству
. Этот пример можно обобщить к пространству  всех непрерывных функций
всех непрерывных функций  , где
, где  — компактное пространство, или к пространству всех ограниченных непрерывных функций
— компактное пространство, или к пространству всех ограниченных непрерывных функций  всех ограниченных функций
всех ограниченных функций  — вещественное число, то пространство всех бесконечных последовательностей
— вещественное число, то пространство всех бесконечных последовательностей  элементов из
элементов из  сходится, является банаховым относительно нормы, равной корню степени
сходится, является банаховым относительно нормы, равной корню степени  из суммы этого ряда, и обозначается
из суммы этого ряда, и обозначается  .
. состоит из всех ограниченных последовательностей элементов из
состоит из всех ограниченных последовательностей элементов из  . Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом:
. Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом: 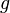 эквивалентны тогда и только тогда, когда норма
эквивалентны тогда и только тогда, когда норма  равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как
равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как  . Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например,
. Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например, 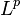 -пространства.
-пространства. — банаховы пространства, то можно составить их прямую сумму
— банаховы пространства, то можно составить их прямую сумму  , которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств.
, которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств.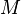 — замкнутое подпространство банахова пространства
— замкнутое подпространство банахова пространства  снова является банаховым.
снова является банаховым. и
и  — банаховы пространства над одним полем
— банаховы пространства над одним полем  обозначается
обозначается 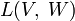 . Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными.
. Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными. 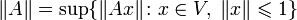 , является также и банаховым.
, является также и банаховым. 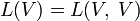 представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений.
представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений. и
и 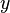 определено скалярное произведение
определено скалярное произведение  и полное относительно порожденной скалярным произведением метрики
и полное относительно порожденной скалярным произведением метрики  . Если условие полноты пространства не выполнено, то говорят о предгильбертовомпространстве. Однако, большинство из известных (используемых) пространств либо являются полными, либо могут быть пополнены.
. Если условие полноты пространства не выполнено, то говорят о предгильбертовомпространстве. Однако, большинство из известных (используемых) пространств либо являются полными, либо могут быть пополнены.