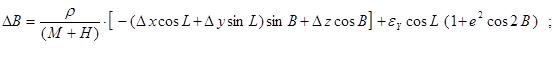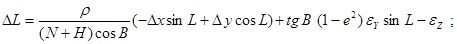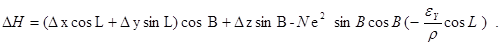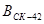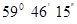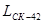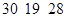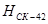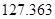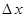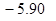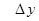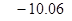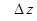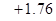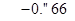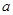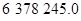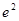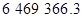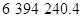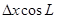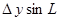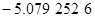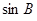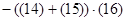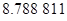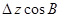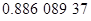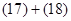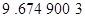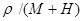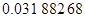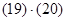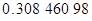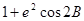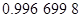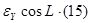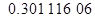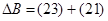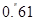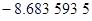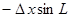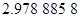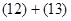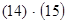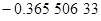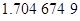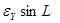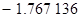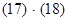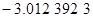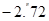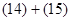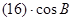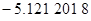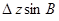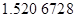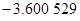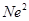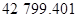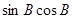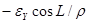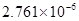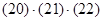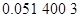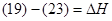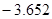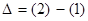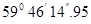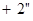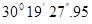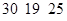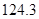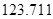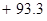Контроль выполнения поэтапного перехода от одной системы координат к другой выполняют, используя следующие зависимости:
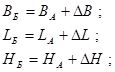
где 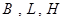 - соответственно геодезические широта и
- соответственно геодезические широта и
долгота, выраженные в угловых единицах, и
геодезическая высота, выраженная в м.;
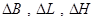 - поправки к геодезическим координатам за
- поправки к геодезическим координатам за
переход от одной системы координат 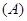 к
к
другой 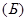 .
.
Поправки к геодезическим координатам определяют по следующим формулам:

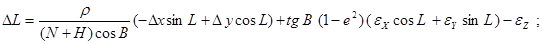
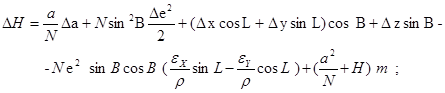
где 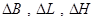 - поправки к геодезическим широте, долготе
- поправки к геодезическим широте, долготе
 , и высоте,
, и высоте, 
 ;
;
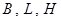 - геодезические широта, долгота,
- геодезические широта, долгота, 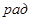 , и
, и
высота,  ;
;
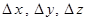 - линейные элементы трансформирования
- линейные элементы трансформирования
системы координат 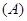 относительно
относительно
системы координат 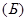 ,
,  ;
;
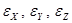 - угловые элементы трансформирования
- угловые элементы трансформирования
системы координат 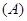 относительно
относительно
системы координат 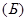 ,
, 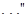 ;
;
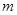 - дифференциальное различие масштабов
- дифференциальное различие масштабов
систем координат 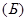 и
и 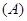 ;
;
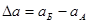 - разность больших полуосей
- разность больших полуосей
эллипсоидов 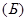 и
и 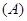 ;
;
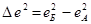 - разность квадратов соответствующих
- разность квадратов соответствующих
эксцентриситетов;
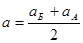 - среднее значение соответствующих больших
- среднее значение соответствующих больших
полуосей;
 - среднее значение квадратов
- среднее значение квадратов
соответствующих первых эксцентриситетов;
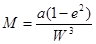 ;
; 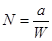 - радиусы кривизны главных нормальных
- радиусы кривизны главных нормальных
сечений;
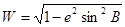 - сфероидическая функция;
- сфероидическая функция;
 - число угловых секунд в 1 радиане.
- число угловых секунд в 1 радиане.
При преобразовании из системы координат 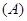 в систему
в систему 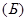 используют значения геодезических координат в системе
используют значения геодезических координат в системе 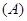 , и наоборот.
, и наоборот.
Суммарные параметры перехода от СК-42 к СК-95, использовавшиеся в практических работах №№ 1,2,3, следующие:
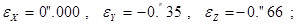
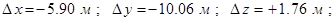
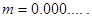
Так как и в СК-42, и в СК-95 принят эллипсоид Красовского, то
 .
.
С учетом параметров перехода, имеющих нулевые значения, формулы для вычисления поправок координат примут следующий вид:
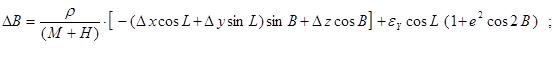
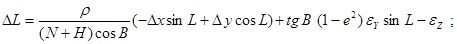
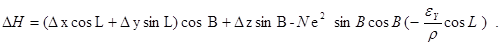
Приведем примеры вычисления по этим формулам:
- вычисление поправки широты (табл.5)
Табл.5 
| №
| Формула, обозначение
| Результат вычисления
| Примечание
|
|
|
|
|
|
|
| 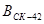
| 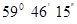
| Широта СК-42
|
|
| 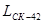
| 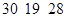
| Долгота СК-42
|
|
| 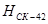
| 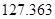
| Высота СК-42
|
|
| 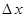
| 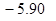
| Смещение абсциссы
|
|
| 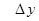
| 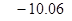
| Смещение ординаты
|
|
| 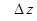
| 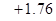
| Смещение аппликаты
|
|
| 
| 
| Поворот относительно оси Y
|
|
| 
| 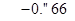
| Поворот относительно оси Z
|
|
| 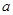
| 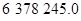
| Большая полуось эллипсоида
|
|
| 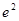
| 
| Квадрат первого
Эксцентриситета
|
|
| 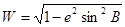
| 
| Сфероидическая функция
|
|
| 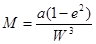 ; ;
|
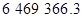
| Радиус кривизны меридианного эллипса
|
|
| 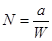 ; ;
|
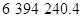
| Радиус кривизны первого вертикала
|
|
| 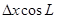
| 
|
|
|
| 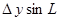
| 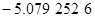
|
|
- вычисление поправки долготы (табл.6)
Табл. 6
| №
| Формула, обозначение
| Результат вычисления
| Примечание
| |
|
| 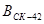
| 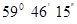
| Широта СК-42
| |
|
| 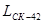
| 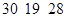
| Долгота СК-42
| |
|
| 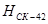
| 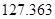
| Высота СК-42
| |
|
| 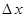
| 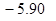
| Смещение абсциссы
| |
|
| 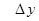
| 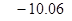
| Смещение ординаты
| |
|
| 
| 
| Поворот относительно оси Y
| |
|
| 
| 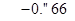
| Поворот относительно оси Z
| |
|
| 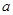
| 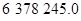
| Большая полуось эллипсоида
| |
|
| 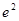
| 
| Квадрат первого
эксцентриситета
| |
|
| 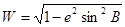
| 
| Сфероидическая функция
| |
|
| 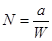 ; ;
| 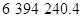
| Радиус кривизны первого вертикала
| |
|
| 
| 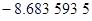 
|
| |
|
| 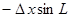
|  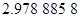
|
| |
|
| 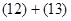
| 
|
| |
|
| 
| 
|
|
| 
|
|
| 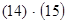
| 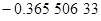
|
|
|
|
| 
| 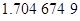
|
| |
|
| 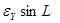
| 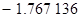
|
| |
|
| 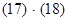
| 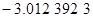
|
| |
|
| 
| 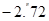
| Поправка долготы
| |
- вычисление поправки высоты (табл.7)
Табл.7
| №
| Формула, обозначение
| Результат вычисления
| Примечание
|
|
| 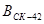
| 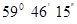
| Широта СК-42
|
|
| 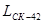
| 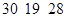
| Долгота СК-42
|
|
| 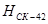
| 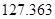
| Высота СК-42
|
|
| 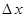
| 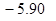
| Смещение абсциссы
|
|
| 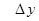
| 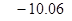
| Смещение ординаты
|
|
| 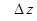
| 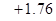
| Смещение аппликаты
|
|
| 
| 
| Поворот относительно оси Y
|
|
| 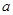
| 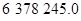
| Большая полуось эллипсоида
|
|
| 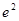
| 
| Квадрат первого
эксцентриситета
|
|
| 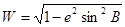
| 
| Сфероидическая функция
|
|
| 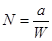 ; ;
|
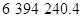
| Радиус кривизны первого вертикала
|
|
| 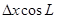
| 
|
|
|
| 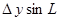
| 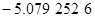
|
|
|
| 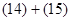
| 
|
|
|
| 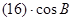
| 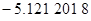
|
|
|
| 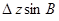
| 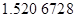
|
|
|
| 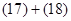
| 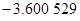
|
|
|
| 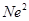
| 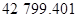
|
|
|
| 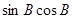
| 
|
|
|
| 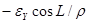
| 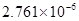
|
|
|
| 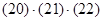
| 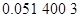
|
|
|
| 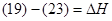
| 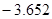
| Поправка высоты
|
Сведем результаты преобразований координат, выполненных двумя способами, в единую ведомость (каталог) (табл.8):
Табл.8
|
| Система СК-42
(исходные
координаты)
| Система СК-95
(последовательное
преобразование)
(1)
| Поправка
| Система СК-95
(контрольное
преобразование)
(2)
| 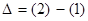
|
| Широта
| 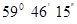
| 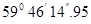
| 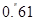
| 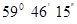
| 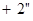
|
| Долгота
| 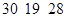
| 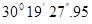
| 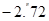
| 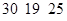
| 
|
| Высота
| 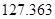
| 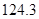
| 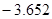
| 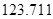
| 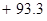
|
Удовлетворительными будем считать сходимость по широте и долготе в пределах 0′′.5 – 3′′.0; по высоте – в пределах 1.0 – 3.0 м.

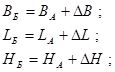
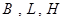 - соответственно геодезические широта и
- соответственно геодезические широта и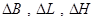 - поправки к геодезическим координатам за
- поправки к геодезическим координатам за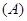 к
к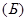 .
.
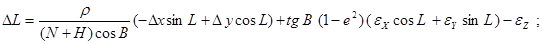
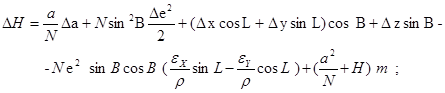
 , и высоте,
, и высоте, 
 ;
;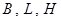 - геодезические широта, долгота,
- геодезические широта, долгота, 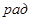 , и
, и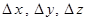 - линейные элементы трансформирования
- линейные элементы трансформирования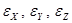 - угловые элементы трансформирования
- угловые элементы трансформирования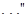 ;
;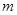 - дифференциальное различие масштабов
- дифференциальное различие масштабов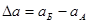 - разность больших полуосей
- разность больших полуосей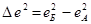 - разность квадратов соответствующих
- разность квадратов соответствующих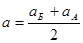 - среднее значение соответствующих больших
- среднее значение соответствующих больших - среднее значение квадратов
- среднее значение квадратов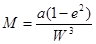 ;
; 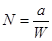 - радиусы кривизны главных нормальных
- радиусы кривизны главных нормальных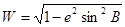 - сфероидическая функция;
- сфероидическая функция; - число угловых секунд в 1 радиане.
- число угловых секунд в 1 радиане.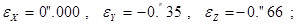
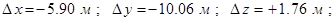
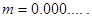
 .
.