Інтерференція від двох когерентних світлових джерел
Розглянемо найпростіший випадок інтерференції монохроматичних світлових хвиль від двох однакових джерел. Припустимо, що ці джерела випромінюють хвилі в однакових фазах. В цьому випадку фази векторів Е 1 = Е 0 sin w то Е = Е 1 + Е 2 = 2 Е 0 В тих точках, де аргумент косинуса дорівнює непарній кількості p / 2, тобто
значення Знайдемо розташування точок, в яких буде відбуватися “гасіння” двох монохроматичних світлових хвиль з однаковою амплітудою Е 0. Оскільки х 2 – х 1 = (2 к +1) Таким чином, в точках, що знаходяться від джерел S 1 і S 2 на відстанях, які задовольняють умові (8.4), світла не буде. Розташування точок, в яких амплітуда сумарної напруженості Е має максимум, визначається умовою cos w звідки х 2 – х 1 = 2 к тобто різниця ходу х 2 – х 1 дорівнює в цьому випадку парній кількості 2 к півхвиль Якщо хвилі 1 і 2 поширювались в різних середовищах до точки, в якій спостерігалася інтерференція, то умови гасіння та підсилення світла виглядатимуть відповідно: х 2 n 2 – x 1 n 1 = (2 к + 1) х 2 n 2 – x 1 n 1 = 2 к де n 1 і n 2 – абсолютні показники заломлення середовищ. Добуток геометричного шляху на показник заломлення, тобто xn, зветься оптичною довжиною шляху, а величина Таким чином, максимуми спостерігаються в тих точках, для яких оптична різниця ходу інтерферуючих хвиль дорівнює парній кількості півхвиль, а мінімуми – в тих точках, для яких оптична різниця ходу дорівнює непарній кількості півхвиль. Необхідно підкреслити, що для постійного взаємного підсилення або гасіння світлових хвиль в будь-якій точці простору різниця фаз хвиль, що надходять в цю точку, не повинна змінюватись з часом. Світлові хвилі однакової довжини, що надходять в певну точку з незмінною в часі різницею фаз, звуться когерентними. Таким чином, лише когерентні хвилі здатні утворювати інтерференційну картину, що не змінюється з часом. Саме тому її можна спостерігати візуально, фотографувати тощо. Два різних джерела невзмозі давати когерентні хвилі через такі причини: 1) збудження елементарних джерел світла (атомів, молекул) внаслідок їх участі в тепловому русі відбувається цілком хаотично, а отже і фази випромінюваних ними світлових хвиль змінюються з часом також хаотично; 2) час випромінювання монохроматичної хвилі, напруженість електричного поля в якій визначається формулою (8.1), триває приблизно tвипр» 10–8 с. За цей час хвиля розповсюджується на відносно коротку відстань
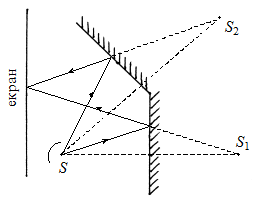
1. За допомогою дзеркал примушують інтерферувати дві частини однієї хвилі (дзеркало Ллойда, мал. 8.2а; подвійне дзеркало Френеля, мал. 8.2б). Результат отримуємо такий самий, як від двох когерентних джерел S 1 і S 2. Насправді точка S 2 в дзеркалі Ллойда і точки S 1 і S 2 в дзеркалі Френеля не є джерелами світла, а являють собою уявні зображення в дзеркалах джерела світла S. 2. В методі біпризми Френеля (мал. 8.2в) світло від джерела S спрямовується на дві тонкі скляні призми, що склеєні своїми основами. Світло, заломлюючись в призмах, утворює два когерентні пучки, котрі перекриваючись, потрапляють на екран, утворюючи інтерференційну картину від двох когерентних джерел, нібито розташованих в точках S 1 і S 2. 3. Використовуються тонкі (прозорі) плівки, на поверхнях яких інтерферують відбиті та заломлені хвилі (мал. 8.3).
Мал. 8.3. Інтерференція заломленої та відбитої хвиль на поверхні тонкої прозорої платівки або плівки. Припустимо, що на прозору плівку товщиною h з показником заломлення n падає плоска хвиля. Знайдемо оптичну різницю ходу променів 1 і 2, що інтерферують в точці с. Опустимо перпендикуляр AD з точки A на промінь 2. Промінь 1, заломлюючись і далі зазнавши відбиття від нижньої границі плівки, пройшов довжину шляху Враховуючи, що при відбитті світла від більш оптично густого середовища фаза хвилі змінюється на p (тобто загублюється півхвилі), для оптичної різниці ходу променів 1 і 2 маємо d = (АВ + ВС) п – (D С + Оскільки АВ + ВС = d = 2 Якщо d = (2 к + 1)
|

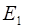 і
і 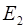 в будь-якій точці залежатимуть від відстаней х 1 і х 2 цієї точки до джерел S 1 і S 2. Отже, якщо
в будь-якій точці залежатимуть від відстаней х 1 і х 2 цієї точки до джерел S 1 і S 2. Отже, якщо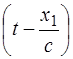 , Е 2 = Е 0 sin w
, Е 2 = Е 0 sin w 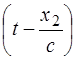 ,
,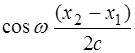
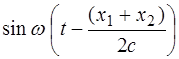 . (8.2)
. (8.2)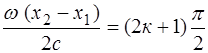 , к = 0, 1, 2,..., (8.3)
, к = 0, 1, 2,..., (8.3)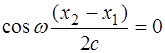 , а отже і результуюча напруженість електричного поля Е в будь-який момент часу дорівнюватиме нулю, тобто світлові хвилі гасять одна одну.
, а отже і результуюча напруженість електричного поля Е в будь-який момент часу дорівнюватиме нулю, тобто світлові хвилі гасять одна одну.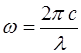 , то з (8.3) маємо
, то з (8.3) маємо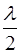 . (8.4)
. (8.4) = 1,
= 1, 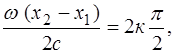
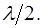 Отже (8.4) є умовою гасіння світла, а (8.5) – його підсилення.
Отже (8.4) є умовою гасіння світла, а (8.5) – його підсилення.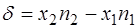 – оптичною різницею ходу інтерферуючих хвиль.
– оптичною різницею ходу інтерферуючих хвиль.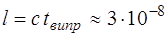 м/с × 10–8 с = 3 м, тобто монохроматична хвиля (інколи кажуть хвильовий цуг) зосереджена в просторовому інтервалі порядка 3 м. Різні джерела одночасно випромінюють безліч монохроматичних хвиль з різними частотами і напрямками коливань напруженості електричного поля. За цих умов ймовірність зустрічі в одній точці простору двох когерентних хвиль з однаковою частотою (довжиною хвилі) практично дорівнює нулю. Тому когерентність інтерферуючих хвиль можливо створювати лише штучно – шляхом розділення кожної хвилі, яка випромінюється джерелом, на дві, що рухаються до місця зустрічі різними шляхами. Для забезпечення когерентності властивості середовища на шляху променів не повинні змінюватись з часом, а оптична різниця їх ходу не повинна перевищувати 3 м. Когерентність світлових променів можна здійснити цілою низкою способів (мал. 8.2 та мал. 8.3).
м/с × 10–8 с = 3 м, тобто монохроматична хвиля (інколи кажуть хвильовий цуг) зосереджена в просторовому інтервалі порядка 3 м. Різні джерела одночасно випромінюють безліч монохроматичних хвиль з різними частотами і напрямками коливань напруженості електричного поля. За цих умов ймовірність зустрічі в одній точці простору двох когерентних хвиль з однаковою частотою (довжиною хвилі) практично дорівнює нулю. Тому когерентність інтерферуючих хвиль можливо створювати лише штучно – шляхом розділення кожної хвилі, яка випромінюється джерелом, на дві, що рухаються до місця зустрічі різними шляхами. Для забезпечення когерентності властивості середовища на шляху променів не повинні змінюватись з часом, а оптична різниця їх ходу не повинна перевищувати 3 м. Когерентність світлових променів можна здійснити цілою низкою способів (мал. 8.2 та мал. 8.3).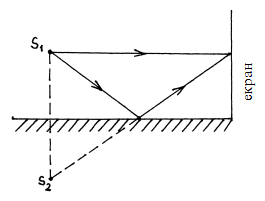

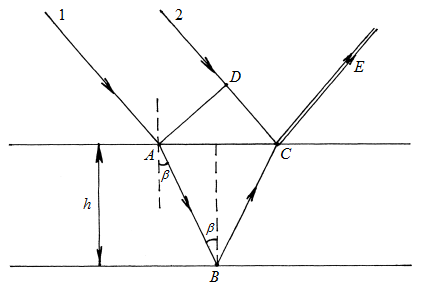
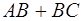 в речовині з показником заломлення n, а промінь 2 – відстань DС в повітрі.
в речовині з показником заломлення n, а промінь 2 – відстань DС в повітрі.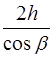 , а DС = АC sin a = 2 h tg b sin a =
, а DС = АC sin a = 2 h tg b sin a = 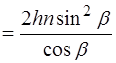 , з (8.6) маємо
, з (8.6) маємо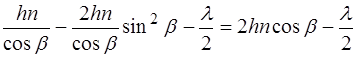 .
.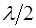 , то промені 1 і 2 в результаті інтерференції в точці С гасять один одного і в напрямку СЕ відбите світло не спостерігається, тобто вся світлова енергія цілком поступає всередину пластинки і від її поверхні не відбивається. Це явище застосовують в складних оптичних системах для “просвітлення оптики” – методу зменшення втрат світла при відбитті, а отже збільшення енергії, що прямує до реєструючих систем – фотоплівок, очей тощо. Практично цього досягають шляхом утворення на поверхнях лінз та призм тонких прозорих плівок з окислу металу. Товщину і показник заломлення плівки підбирають таким чином, щоб промені, відбиті від зовнішньої і внутрішньої поверхонь плівки, взаємно гасили один одного.
, то промені 1 і 2 в результаті інтерференції в точці С гасять один одного і в напрямку СЕ відбите світло не спостерігається, тобто вся світлова енергія цілком поступає всередину пластинки і від її поверхні не відбивається. Це явище застосовують в складних оптичних системах для “просвітлення оптики” – методу зменшення втрат світла при відбитті, а отже збільшення енергії, що прямує до реєструючих систем – фотоплівок, очей тощо. Практично цього досягають шляхом утворення на поверхнях лінз та призм тонких прозорих плівок з окислу металу. Товщину і показник заломлення плівки підбирають таким чином, щоб промені, відбиті від зовнішньої і внутрішньої поверхонь плівки, взаємно гасили один одного.


