Ідеальна центрована оптична система
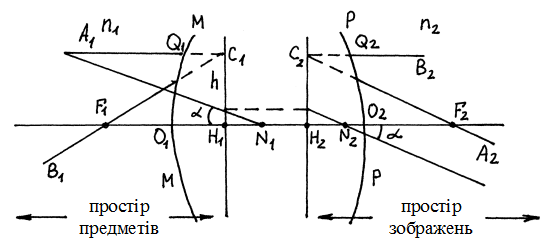
Система сферичних поверхонь (лінз) називається центрованою, якщо центри всіх сферичних поверхонь лежать на одній прямій, яка має назву головної оптичної вісі системи. Згідно з теорією оптичних систем, яка була розроблена відомим німецьким математиком Гауссом, ідеальною оптичною системою є система, в якій зображення є подібним предмету, тобто будь-якій точці чи лінії простору предметів відповідає одна і тільки одна точка чи лінія простору зображень. Такі точки та лінії називаються спряженими. Аналогічно, кожній площині простору предметів (об’єктів) повинна відповідати спряжена площина простору зображень. Таким чином, теорія ідеальних оптичних систем є чисто геометричною теорією, яка встановлює зв’язок між точками, лініями і площинами. Ідеальною оптичною системою з достатнім ступенем точності можна вважати центровану, якщо обмежитись областю поблизу вісі симетрії – головної оптичної вісі. Промені, що розповсюджуються поблизу головної оптичної вісі, звуться параксіальними. Теорія Гаусса встановлює зв’язок між так званими кардинальними точками і площинами, завдання яких повністю описує всі властивості центрованої оптичної системи (ЦОС) і дозволяє користуватись нею, не розглядаючи реального ходу променів у цій системі. Нехай ММ і РР – крайні сферичні поверхні, що обмежують нашу систему, О 1 О 2 – її головна вісь, n 1 і n 2 – показники заломлення середовищ (мал. 8.13). З променем А 1, паралельним О 1 О 2, спряжений промінь А 2, який проходить через точку F 2 (згідно з властивостями ідеальної системи). Візьмемо інший промінь О 1 вздовж головної оптичної осі.
Мал. 8.13. Кардинальні точки і площини ЦОС. Спряжений з ним промінь О 2 йтиме також вздовж головної осі. Точка F 2 – точка перетину двох променів А 2 і О 2, є зображенням точки, в якій перетинаються промені А 1 і О 1, спряжені з А 2 і О 2. Оскільки А 1 паралельний О 1, то точка, що спряжена з F 2, лежить на нескінченності. Таким чином, точка F 2 – це фокус даної системи, розташований в просторі зображень. Аналогічно променю В 2 спряжений промінь В 1, який проходить через передній фокус системи F 1. Площина, яка проходить через фокус перпендикулярно О 1 О 2, називається фокальною. Оскільки промені А 1 і В 1 спряжені з променями А 2 і В 2, то спряженими виявляються точки перетину цих променів – С 1 і С 2. Через С 1 і С 2 проведемо площини перпендикулярно до головної оптичної вісі, які перетнуть її в точках Н 1 і Н 2. Ці точки також є спряженими і називаються головними точками. Площини, які проходять через ці точки перпендикулярно до головної оптичної вісі, називаються головними площинами. Вони відзначаються тим, що промінь, який падає на одну площину в точці С 1 на відстані h від головної вісі, виходить із другої площини в точці С2, розташованій на такій самій відстані від осі. Таким чином, відрізки | С 1 Н 1| = | С 2 Н 2| = h, тобто лінійне збільшення цих відрізків дорівнює одиниці. Головні точки і фокуси називаються ще кардинальними точками ЦОС, а площини, які проходять через них і перпендикулярні О 1 О 2 - кардинальними площинами. Віддаль від головних точок до фокусів називається фокусною віддаллю системи: [ F 1 H 1] = f 1, [ F 2 H 2] = f 2. Існують також ще одна пара кардинальних точок N 1 i N 2, які звуться вузлові,або нодальні. Їх особливість полягає в тому, що спряжені промені, які проходять через ці точки, мають однаковий кут нахилу до оптичної вісі. Якщо показники заломлення простору предметів та простору зображень є однаковими (n 1 = n 2), то вузлові точки співпадають з відповідними головними точками. Отже, в ЦОС виділяють шість кардинальних точок: дві – фокуси (F 1 і F 2), дві головні (H 1 і H 2) і дві вузлові (N 1 і N 2) і, відповідно, шість кардинальних площин. У тонкій лінзі, яка є частковим випадком ЦОС, є три кардинальні точки, оскільки головні і вузлові точки співпадають з оптичним центром. Як приклад, розглянемо побудову зображення точкового джерела світла S 1 (мал. 8.14).
Мал. 8.14. Побудова зображення точки в ЦОС. Промінь із світлової точки S 1, паралельний головній оптичній вісі, проводимо до перетину з головною площиною простору зображень, а потім через другий фокус F 2. Промінь 2 йде через перший фокус F 1 до головної площини простору предметів, а потім паралельно головній оптичній вісі. Перетин променів 1 і 2 у просторі зображень дає зображення S 2 світлової точки S 1. Можна навести формули, які зв’язують положення предмету і його зображення:
де а 1 і а 2 – відстані від предмета до головної площини простору предметів і від головної площини простору зображень до зображення предмета відповідно, f 1 i f 2 – фокусні відстані, а n 1 i n 2 – показники заломлення середовищ. Важливим елементом оптичних систем, які утворюють зображення предмета, є оптична діафрагма – це отвір у непрозорому тілі, який обмежує ширину пучка світлових променів, центр якого лежить на головній вісі оптичної системи. Діафрагма, яка найбільш сильно обмежує світловий пучок (незалежно від місця її знаходження в оптичній системі), називається апертурною діафрагмою. Такою діафрагмою може служити край чи оправа лінзи, наприклад, об’єктива. Ця діафрагма обмежує ширину оптичних пучків, а також не пропускає в оптичну систему промені, що падають на лінзу під великими кутами до головної оптичної вісі. Вона підвищує чіткість зображення і сприяє усуненню аберацій та, водночас, обмежує кількість світлових променів, які попадають в оптичну систему, тобто зменшує яскравість зображення. Кут q, який рівний половині кута, утвореного двома крайніми променями, що падають в отвір апертурної діафрагми з точки перетину площини предмета з головною оптичною віссю, називається апертурним кутом оптичної системи.
|


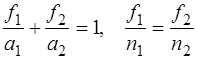 ,
,


