Дифракція на щілині в паралельних променях
При перпендикулярному падінні світла на площину щілини шириною а всі точки фронту хвилі АВ коливаються в однаковій фазі. Тому промені, які не змінили свого напрямку, не мають різниці ходу і, фокусуючись лінзою в точці О екрану, дають максимум освітленості (мал. 8.9).
Мал. 8.9. Дифракція на щілині в паралельних променях. Промені, які внаслідок дифракції відхилились на кут j від напрямку променів, що падають на щілину, набувають різницю ходу d. Визначимо цю різницю ходу, побудувавши фронт хвилі для цих променів. Для цього з точки А опустимо перпендикуляр на промінь, що виходить з точки В. Очевидно, що різниця ходу d дорівнює довжині відрізка ВС. Розіб’ємо ВС на відрізки величиною n = Число n може бути парним і непарним. Якщо n – парне число, то результатом інтерференції вторинних хвиль буде мінімум, оскільки в кожних двох сусідніх зонах маємо симетрично розташовані промені з sin j min = Якщо n = (2 к + 1) (остання зона може бути і неповною), то в точці О 1 спостерігатиметься максимум, тобто напрямок на максимум визначається умовою а sin j max = (2 к + 1) sin j max = З формули (8.9) маємо: 1) за умови а >> l,sin j max @ 0, тобто кут дифракції j малий, і явище дифракції важко спостерігати; 2) за умови а << l,sin j max @ 1, звідки
|


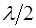 . Якщо провести з точок поділу прямі паралельні АС, фронт хвилі в щілині АВ виявиться поділеним на зони, які називаються зонами Френеля. Вторинні хвилі, що йдуть від симетричних точок сусідніх зон Френеля, гасять одна одну. Для даних ширини щілини а і довжини хвилі l кількість зон n залежить від кута j відхилення променів
. Якщо провести з точок поділу прямі паралельні АС, фронт хвилі в щілині АВ виявиться поділеним на зони, які називаються зонами Френеля. Вторинні хвилі, що йдуть від симетричних точок сусідніх зон Френеля, гасять одна одну. Для даних ширини щілини а і довжини хвилі l кількість зон n залежить від кута j відхилення променів . (8.7)
. (8.7) , котрі, інтерферуючи в точці О 1, гасять один одного. Таким чином, напрямок на мінімум визначається умовою n = 2 к, де
, котрі, інтерферуючи в точці О 1, гасять один одного. Таким чином, напрямок на мінімум визначається умовою n = 2 к, де  . (8.8)
. (8.8) . (8.9)
. (8.9) , тобто весь екран буде освітленим і не спостерігатиметься чергування максимумів і мінімумів. Очевидно, що для спостерігання дифракційної картини необхідне виконання умови а» l.
, тобто весь екран буде освітленим і не спостерігатиметься чергування максимумів і мінімумів. Очевидно, що для спостерігання дифракційної картини необхідне виконання умови а» l.


