Дифракційна решітка
Явище дифракції можна використовувати для дослідження спектрів випромінювання і поглинання, а також визначення довжини хвилі. Для цього використовується дифракційна решітка – оптичний пристрій, що являє собою сукупність великої кількості паралельних вузьких щілин. Решітка створюється шляхом нанесення подряпин (штрихів) на скляну платівку. Проміжки між штрихами – це щілини, що пропускають світло. Позначимо ширину щілини а, а проміжок між щілинами – b. Величину d = a + b називають періодом дифракційної решітки. При падінні світла на дифракційну решітку у всіх щілинах виникають вторинні когерентні хвилі, які внаслідок дифракції утворюють в фокальній площині лінзи інтерференційну картину (мал. 8.10), що складається з великої кількості максимумів і мінімумів різної інтенсивності. Ця картина відтворює інтерференцію як променів, що пройшли кожну окрему щілину, так і променів, що пройшли різні щілини і падають на лінзу під однаковими кутами. Останні і утворюють найбільш інтенсивні максимуми, що звуться головними.
Мал. 8.10. Дифракція плоскої хвилі на дифракційній решітці. Розглянемо симетричні промені, що йдуть з сусідніх щілин. Якщо різниця ходу d цих променів дорівнює цілому числу довжин хвиль, то на екрані в результаті інтерференції цих хвиль виникає максимум. При цьому d = АС = кl,але АС = d sin j, отже d sin j = кl,(8.10) де к – порядок максимуму (к = 0, 1, 2, …). Співвідношення (8.10) називають формулою дифракційної решітки. Головні максимуми розташовані симетрично відносно центрального максимуму (j = 0). Можна показати, що між двома головними максимумами спостерігається N – 1 мінімум, де N – кількість щілин в решітці. Головні максимуми на інтерференційній картині значно вужчі і різкіші, ніж при дифракції на одній щілині. Із збільшенням кількості щілин N окремі додаткові мінімуми майже не розрізняються і проміжки між головними максимумами стають темними, а головні максимуми – різкішими. При падінні на решітку білого чи немонохроматичного світла кожний максимум, окрім центрального, розкладається в спектр. В цьому випадку значення к вказує на порядок спектра. Головними характеристиками дифракційної решітки як оптичного приладу є кутова дисперсія D і роздільна здатність R. Нехай кутова відстань між двома лініями спектру, що відрізняються по довжині хвилі на dl, дорівнює dj. Величину Продиференціюємо формулу дифракційної решітки (8.10) d cosj dj = к dl, звідки D = тобто кутова дисперсія тим більша, чим менший період решітки d і більший порядок спектра к. Можливість розрізняти близькі лінії залежить не лише від ширини спектра, тобто від D, але й від ширини окремих ліній, котрі можуть накладатися одна на одну. Розрізнення спектральних ліній оцінюють роздільною здатністю R, яка дорівнює відношенню довжини хвилі до найменшого інтервалу довжин хвиль, котрі можуть бути розрізнені: R = Якщо R = кN, тобто роздільна здатність дифракційної решітки збільшується із зростанням кількості штрихів N і порядку спектра к. Згідно з принципом Релея, дві спектральні лінії розрізняються, якщо максимум однієї лінії співпадає з найближчим мінімумом іншої лінії (мал. 8.11) або знаходиться на більшій відстані від нього.
|


 називають кутовою дисперсією. Кутова дисперсія чисельно дорівнює першій похідній від кута відхилення променів по довжині хвилі або кутовій відстані між двома лініями спектра, які відповідають довжинам хвиль, що відрізняються на одиницю. Кутова дисперсія визначає ширину спектра.
називають кутовою дисперсією. Кутова дисперсія чисельно дорівнює першій похідній від кута відхилення променів по довжині хвилі або кутовій відстані між двома лініями спектра, які відповідають довжинам хвиль, що відрізняються на одиницю. Кутова дисперсія визначає ширину спектра.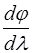 =
=  ,
, .
. l 1@ l 2, а D l = l 1 – l 2, то
l 1@ l 2, а D l = l 1 – l 2, то  або
або  . Розрахунки показують, що
. Розрахунки показують, що



