Число микросостояний (термодинамическая вероятность) и
Энтропия Тенденция к уменьшению энергосодержания, т.е. уменьшению энтальпии системы, при р=const не является единственным фактором, определяющим направление самопроизвольного протекания реакции в данных условиях. Вероятно, существуют две движущие силы самопроизвольного процесса: одна стремится уменьшить энергосодержание системы с выделением теплоты, и какая-то вторая сила, в ряде случаев превосходящая первую. Для изучения этой силы рассмотрим процесс смешения двух газов, не реагирующих между собой. Пусть два инертных газа – гелий и неон – находятся при одинаковой температуре и давлении в двух одинаковых частях сосуда, разделенных перегородкой (состояние 1) (рис. 3.3).
Рис. 3.3. Процесс смешения газов Удалим перегородку, не изменяя энергетического запаса системы. Хотя давление газов в обеих частях сосуда было одинаковым, начнется процесс смешения газов, и через некоторое время молекулы гелия и неона будут равномерно распределены по всему объему системы (состояние 2). Процесс смешения газов, т.е. переход их из состояния 1 в состояние 2, проходил без изменения энтальпии, так как при комнатной температуре какое-либо взаимодействие между молекулами инертных газов практически отсутствует. Газы, разделенные перегородкой (состояние 1), распределены в системе с бóльшим порядком по сравнению со смесью газов (состояние 2). По-видимому, движущей силой смешения газов является тенденция перехода в более хаотичное состояние. В химической термодинамике применяют обычно выражения «беспорядок» или «степень беспорядка», т.е. степень беспорядка 2 > степени беспорядка 1. Самопроизвольный процесс, проходящий без изменения энергетического состояния изолированной системы, совершается только в направлении, при котором система переходит в более вероятное (хаотичное) состояние. Химическая термодинамика изучает системы реагирующих веществ, состоящие из очень большого числа частиц. В подобных системах различают так называемые макро – и микропараметры. К макрохарактеристикам относятся независимые переменные, свойственные системе в целом, например, давление, объем, температура. Макроскопическое (наблюдаемое) состояние системы, характеризуемое определенными термодинамическими параметрами, может существовать при различном распределении молекул, т.е. оно осуществляется разными микросостояниями, отличающимися друг от друга по определенному признаку (например, по координатам x, y, z каждой молекулы в пространстве, скорости, энергии). Вероятность каждого макросостояния пропорциональна числу микросостояний, которыми оно осуществляется. Рассмотрим следующий пример. Пусть система состоит из двух молекул идеального газа, которые находятся в объеме, состоящем из N маленьких объемов, каждый из которых соизмерим с размером молекулы (т.е. в каждом микрообъеме может быть одна молекула). На схеме эти объемы изображены в виде клеток. Допустим, наша система состоит из 5 клеток («микрообъемов»). Размещения проведем следующим образом: одну молекулу помещаем в 1−ю клетку, а вторую – попеременно во 2−ю или в 3−ю, 4−ю или в 5−ю. Таким образом, число размещений двух молекул при условии, что одна молекула находится в 1−й клетке, будет 4. Затем одну молекулу помещаем во вторую клетку, а другую − в 3−ю, 4−ю или в 5−ю и т.д.
В общем случае число размещений (CxN) x молекул по N клеткам, при условии, что x < N равно:
Число микросостояний (или способов) которыми может быть реализовано данное макросостояние системы,называется термодинамической вероятностью (W).
Для больших x и N:
Объем системы равен V / v, где v − величина одного микрообъема. Отсюда N = V / v. Тогда отношение количества микросостояний для двух систем с разным объемом, т.е. разным числом микрообъемов N, при одинаковом количестве молекул х будет:
Для 1 моля газа х = N a=6,02
Термодинамические вероятности выражаются очень большими числами и практически пользоваться им неудобно. Поэтому более целесообразным оказалось характеризовать степень беспорядка системы величиной энтропии. Понятие энтропии ввел в науку Р. Клаузиус, теоретически исследуя работу тепловой машины. Связь энтропии с термодинамической вероятностью установил Л. Больцман, соответствующее уравнение (3.8) названо его именем: S = k ln W, (3.8) где S − энтропия; размерность энтропии Таким образом, энтропия количественно характеризует термодинамическую вероятность того или иного состояния индивидуального вещества или системы.
|



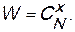 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) 1023.
1023. (3.7)
(3.7) ; W − термодинамическая вероятность; k − константа Больцмана,
; W − термодинамическая вероятность; k − константа Больцмана,  = 1,38
= 1,38 


