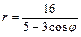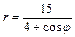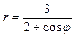И аналитической геометрии. ПРАКТИЧЕСКАЯ ЧАСТЬ1.Задание (условие задачи)2
Федеральное государственное образовательное учреждение Высшего профессионального образования «Сибирский федеральный университет» ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА МАТЕМАТИКА КОНТРОЛЬНЫЕ ЗАДАНИЯ Для студентов-заочников всех специальностей Красноярск СФУ 2012
Высшая математика: Контрольные задания для студентов-заочников всех специальностей академии / Сост. А. Т. Автухова, С.И. Осипова (переработано и дополнено); СФУ. - Красноярск, 2012. - 41 с.
Элементы векторной алгебры и аналитической геометрии
1 – 10. Даны векторы
11 – 20. Даны координаты вершин пирамиды А 1 А 2 А 3 А 4. Найти: 11. А 1 (2; 1; –4), А 2(1; –2; 3), А 3(1; –2; –3), А 4(5; –2; 1). 12. А 1 (2; –1; 3), А 2 (–5; 1; 1), А 3(0; 3; –4), А 4(–1; –3; 4). 13. А 1 (5; 3; 6), А 2 (–3; –4; 4), А 3(5; –6;8), А 4(4; 0; –3). 14. А 1 (5; 2; 4), А 2(–3; 5; –7), А 3(1; –5; 8), А 4(9; –3; 5). 15. А 1 (7; –1; –2), А 2(1; 7; 8), А 3(3; 7; 9), А 4(–3; –5; 2). 16. А 1 (–2; 3; 4), А 2(4; 2; –1), А 3(2; –1; 4), А 4(–1; –1; 1). 17. А 1 (0; 4; –4), А 2(5; 1; –1), А 3(–1; –1; 3), А 4(0; –3; 7). 18. А 1 (0; –6; 3), А 2(3; 3; –3), А 3(–3; –5; 2), А 4(–1; –4; 0). 19. А 1 (2; –1; 3), А 2(–5; 1; 1), А 3(0; 3; –4), А 4(–1; –3; 4). 20. А 1 (2; 1; –4), А 2(1; –2; 3), А 3(1; –2; –3), А 4(5; –2; 1). 21. Даны вершины треугольника: А (1; –1), В (–2; 1), С (3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из вершины В. 22. Даны вершины треугольника: А (2; 1), В (–1; –1), С (3; 2). Составить уравнения его высот. 23. Составить уравнения сторон и медиан треугольника с вершинами А (3; 2), В (5; –2), С (1; 0). 24. Даны вершины треугольника: А (1; 4), В (3; –9), С (–5; 2). Определить длину его медианы, проведенной из вершины В. 25. Даны три вершины А (2; 3), В (4; –1), С (0; 5) параллелограмма АВСD. Найти его четвертую вершину D, противоположную вершине В. 26. Даны вершины четырехугольника: А (–2; 14), В (4; –2), С (6; –2), D (6; 10). Определить точку пересечения его диагоналей АС и ВD. 27. Даны уравнения двух сторон параллелограмма 8 х + 3 у + 1 = 0, 2 х + у – 1 = 0 и уравнение одной из его диагоналей 3 х + 2 у + 3 = 0. Определить координаты вершины этого параллелограмма т.р. (–5, 13). 28. Найти точку Q, симметричную относительно прямой 29. Даны уравнения двух сторон параллелограмма х – 2 у = 0, х – у – 1 = 0 и точка пересечения его диагоналей М (3; –1). Найти уравнения двух других сторон параллелограмма. 30. Даны уравнения двух сторон прямоугольника 5 х + 2 у –7= 0, 5 х + 2 у – 36 = 0 и уравнение его диагонали 3 х + 7 у – 10 = 0. Составить уравнения остальных сторон этого прямоугольника.
31 – 40. Привести уравнение кривой второго порядка к каноническому виду, построить график кривой. 31. x 2 + у 2 – 4 x + 2 у = 4; 32. x 2 – у 2 – 4 у – 13 = 0; 33. x 2 – 4 x + 2 у + 2= 0; 34. x 2 + 4 x + 4 у 2 + 8у – 5 = 0; 35. x 2 – 6 у 2 – 12 x + 36 у – 54 = 0; 36. 2 x 2 + 4 x + 18 у 2 – 16= 0; 37. 2 x 2 + 2 у 2+ 4 x – 8 у – 8 = 0; 38. – x + у 2 + 2 у = 0; 39. 3 x 2 + 5 у 2 + 12 x – 10 у + 2 = 0; 40. 4 x 2 – 3 у 2 – 8 x – 6 у – 11 = 0.
41 – 50. Линия задана уравнением r = r (j) в полярной системе координат. Требуется: 1) построить линию по точкам начиная от j=0 до j=2p и придавая j значения через промежутки p/8; 2) по рисунку определить тип линии.
|

 (а 1; а 2; а 3),
(а 1; а 2; а 3),  (b 1; b 2; b 3),
(b 1; b 2; b 3),  (c 1; c 2; c 3) и
(c 1; c 2; c 3) и  (d 1; d 2; d 3) в некотором базисе. Показать, что векторы
(d 1; d 2; d 3) в некотором базисе. Показать, что векторы 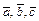 образуют базис и найти координаты вектора d в этом базисе.
образуют базис и найти координаты вектора d в этом базисе. (3; 1; 4),
(3; 1; 4),
 (1; 2; –3),
(1; 2; –3),