И математическая статистика
351. Среди 25 студентов группы, в которой десять девушек, разыгрывается пять билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки.
352. В лотерее разыгрывается 1000 билетов. Среди них два выиграша по 500 руб., пять по 200 руб., десять по 100 руб. и 25 по 50 руб. Некто покупает один билет. Найти вероятность: 1) выигрыша не менее 200 руб.; б) какого-либо выигрыша.
353. Техническое устройство, состоящее из трёх узлов, работало в течение некоторого времени t. За это время первый узел оказывается неисправным с вероятностью 0,1, второй с вероятностью 0,15, третий – с вероятностью 0,05. Найти вероятность того, что за время работы хотя бы один узел технического устройства станет неисправным.
354. Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится: а) только в одном справочнике; б) только в двух справочниках; в) во всех трёх справочниках.
355. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9; для велосипедиста – 0,8; для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
356. Имеется 3 коробки деталей, изготовленных заводом №1 и 2 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартная равна 0,8, а завода №2 – 0,9. Сборщик наудачу извлёк деталь из наудачу взятой коробки. Найти вероятность того, что наудачу извлечённая деталь из наудачу взятого ящика стандартная.
357. В четырёх попытках разыгрываются некоторые предметы. Вероятность выиграша в каждой попытке равна 0,5. Какова вероятность выиграша трёх предметов?
358. Предприятие изготовило и отправило заказчику 100000 бутылок минеральной воды. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет пять битых бутылок.
359. В микрорайоне девять машин технической службы. Для бесперебойной работы необходимо, чтобы не менее восьми машин были в исправном состоянии. Считая вероятность исправного состояния для всех машин одинаковой и равной 0,9, найти вероятность бесперебойной работы технической службы в микрарайоне.
360. Фирма рассылает рекламные проспекты восьми потенциальным партнерам. В результате такой рассылки в среднем у каждого пятого потенциального партнера возникает интерес к фирме. Найти вероятность того, что это произойдет не более чем в трёх случаях.
361 – 370. Дискретная случайная величина X может принимать только два значения: 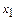 и и 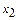 , причем , причем 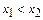 . Известны вероятность . Известны вероятность 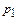 возможного значения возможного значения 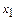 , математическое ожидание , математическое ожидание 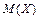 и дисперсия и дисперсия 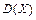 . Найти закон распределения этой случайной величины. . Найти закон распределения этой случайной величины.
361. 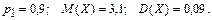
362. 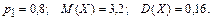
363. 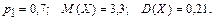
364. 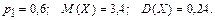
365. 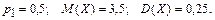
366. 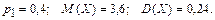
367. 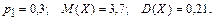
368. 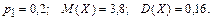
369. 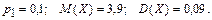
370. 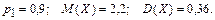
371 – 380. Случайная величина Х задана функцией распределения 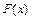 . Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. . Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
| 371.
| 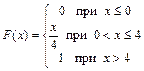
| 372.
| 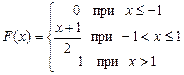
| | | 373.
| 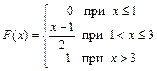
| 374.
| 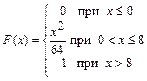
| | | 375.
| 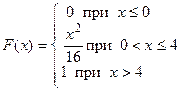
| 376.
| 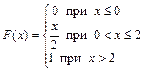
| | 377.
| 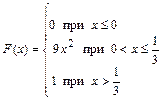
| 378.
| 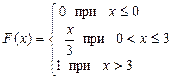
| | | 379.
| 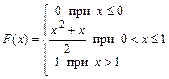
| 380.
| 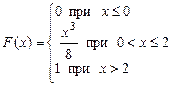
| | | | | | | | | |
381 – 390. Известны математическое ожидание а и среднее квадратическое отклонение s нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (a; b).
381.  382. 382. 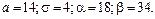
383. 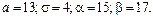 384. 384. 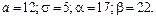
385. 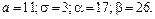 386. 386. 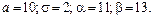
387. 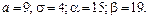 388. 388. 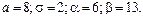
389. 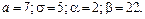 390. 390. 
391 – 400. Расчетное задание включает предварительную обработку статистики, построение линейной регрессионной модели:
1. Найти объем выборок, относительные частоты и накопленные относительные частоты. Если случайная величина (СВ) задана интервалами, то определить середины интервалов.
2. Построить полигон частот, гистограмму для СВ.
3. Найти эмпирическую функцию распределения, построить график.
4. Определить числовые оценки параметров распределения.
5. Построить доверительный интервал для математического ожидания и среднеквадратического отклонения.
6. Провести корреляционный анализ (определить коэффициент корреляции и его значимость). Построить линейные регрессионные зависимости.
391.
| x
y
| 1,15
1,22
| 1,22
1,29
| 1,29
1,36
| 1,36
1,43
| 1,43
1,5
| 1,5
1,57
| 1,57
1,64
| 1,64
1,71
| 1,71
1,78
| 
| | 74,5
81,5
|
|
|
|
|
|
|
|
|
|
| | 81,5
88,5
|
|
|
|
|
|
|
|
|
|
| | 88,5
95,5
|
|
|
|
|
|
|
|
|
|
| | 95,5
102,5
|
|
|
|
|
|
|
|
|
|
| | 102,5
109,5
|
|
|
|
|
|
|
|
|
|
| | 109,5
116,5
|
|
|
|
|
|
|
|
|
|
| | 116,5
123,5
|
|
|
|
|
|
|
|
|
|
| | 123,5
130,5
|
|
|
|
|
|
|
|
|
|
| | 130,5
137,5
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
392.
| x
y
| 1,78
1,85
| 1,85
1,92
| 1,92
1,99
| 1,99
2,06
| 2,06
2,13
| 2,13
2,2
| 2,2
2,27
| 2,27
2,34
| 2,34
2,41
| 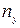
| | 137,5
144,5
|
|
|
|
|
|
|
|
|
|
| | 144,5
151,5
|
|
|
|
|
|
|
|
|
|
| | 151,5
158,5
|
|
|
|
|
|
|
|
|
|
| | 158,5
165,5
|
|
|
|
|
|
|
|
|
|
| | 165,5
172,5
|
|
|
|
|
|
|
|
|
|
| | 172,5
179,5
|
|
|
|
|
|
|
|
|
|
| | 179,5
186,5
|
|
|
|
|
|
|
|
|
|
| | 186,5
193,5
|
|
|
|
|
|
|
|
|
|
| | 193,5
200,5
|
|
|
|
|
|
|
|
|
|
| 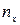
|
|
|
|
|
|
|
|
|
|
| 393.
| x
y
| 2,41
2,48
| 2,48
2,55
| 2,55
2,62
| 2,62
2,69
| 2,69
2,76
| 2,76
2,83
| 2,83
2,9
| 2,9
2,97
| 2,97
3,04
| 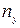
| | 200,5
207,5
|
|
|
|
|
|
|
|
|
|
| | 207,5
214,5
|
|
|
|
|
|
|
|
|
|
| | 214,5
221,5
|
|
|
|
|
|
|
|
|
|
| | 221,5
228,5
|
|
|
|
|
|
|
|
|
|
| | 228,5
235,5
|
|
|
|
|
|
|
|
|
|
| | 235,5
242,5
|
|
|
|
|
|
|
|
|
|
| | 242,5
249,5
|
|
|
|
|
|
|
|
|
|
| | 249,5
256,5
|
|
|
|
|
|
|
|
|
|
| | 256,5
263,5
|
|
|
|
|
|
|
|
|
|
| 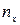
|
|
|
|
|
|
|
|
|
|
|
394.
| x
y
| 3,04
3,11
| 3,11
3,18
| 3,18
3,25
| 3,25
3,32
| 3,32
3,39
| 3,39
3,46
| 3,46
3,53
| 3,53
3,6
| 3,6
3,67
| 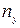
| | 263,5
270,5
|
|
|
|
|
|
|
|
|
|
| | 270,5
277,5
|
|
|
|
|
|
|
|
|
|
| | 277,5
284,5
|
|
|
|
|
|
|
|
|
|
| | 284,5
291,5
|
|
|
|
|
|
|
|
|
|
| | 291,5
298,5
|
|
|
|
|
|
|
|
|
|
| | 298,5
305,5
|
|
|
|
|
|
|
|
|
|
| | 305,5
312,5
|
|
|
|
|
|
|
|
|
|
| | 312,5
319,5
|
|
|
|
|
|
|
|
|
|
| | 319,5
326,5
|
|
|
|
|
|
|
|
|
|
| 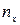
|
|
|
|
|
|
|
|
|
|
| 395.
| x
y
| 3,67
3,74
| 3,74
3,81
| 3,81
3,88
| 3,88
3,95
| 3,95
4,02
| 4,02
4,09
| 4,09
4,16
| 4,16
4,23
| 4,23
4,3
| 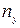
| | 326,5
333,5
|
|
|
|
|
|
|
|
|
|
| | 333,5
340,5
|
|
|
|
|
|
|
|
|
|
| | 340,5
347,5
|
|
|
|
|
|
|
|
|
|
| | 347,5
354,5
|
|
|
|
|
|
|
|
|
|
| | 354,5
361,5
|
|
|
|
|
|
|
|
|
|
| | 361,5
368,5
|
|
|
|
|
|
|
|
|
|
| | 368,5
375,5
|
|
|
|
|
|
|
|
|
|
| | 375,5
382,5
|
|
|
|
|
|
|
|
|
|
| | 382,5
389,5
|
|
|
|
|
|
|
|
|
|
| 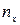
|
|
|
|
|
|
|
|
|
|
|
396.
| x
y
| 4,3
4,37
| 4,37
4,41
| 4,41
4,51
| 4,51
4,58
| 4,58
4,65
| 4,65
4,72
| 4,72
4,79
| 4,79
4,86
| 4,86
4,93
| 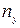
| | 389,5
396,5
|
|
|
|
|
|
|
|
|
|
| | 396,5
403,5
|
|
|
|
|
|
|
|
|
|
| | 403,5
410,5
|
|
|
|
|
|
|
|
|
|
| | 410,5
417,5
|
|
|
|
|
|
|
|
|
|
| | 417,5
424,5
|
|
|
|
|
|
|
|
|
|
| | 424,5
431,5
|
|
|
|
|
|
|
|
|
|
| | 431,5
438,5
|
|
|
|
|
|
|
|
|
|
| | 438,5
445,5
|
|
|
|
|
|
|
|
|
|
| | 445,5
452,5
|
|
|
|
|
|
|
|
|
|
| 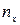
|
|
|
|
|
|
|
|
|
|
| 397.
| x
y
| 4,93
5,00
| 5,00
5,07
| 5,07
5,14
| 5,14
5,21
| 5,21
5,28
| 5,28
5,35
| 5,35
5,42
| 5,42
5,49
| 5,49
5,56
| 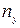
| | 452,5
459,5
|
|
|
|
|
|
|
|
|
|
| | 459,5
466,5
|
|
|
|
|
|
|
|
|
|
| | 466,5
473,5
|
|
|
|
|
|
|
|
|
|
| | 473,5
480,5
|
|
|
|
|
|
|
|
|
|
| | 480,5
487,5
|
|
|
|
|
|
|
|
|
|
| | 487,5
494,5
|
|
|
|
|
|
|
|
|
|
| | 494,5
501,5
|
|
|
|
|
|
|
|
|
|
| | 501,5
508,5
|
|
|
|
|
|
|
|
|
|
| | 508,5
515,5
|
|
|
|
|
|
|
|
|
|
| 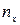
|
|
|
|
|
|
|
|
|
|
|
398.
| x
y
| 5,56
5,63
| 5,63
5,70
| 5,70
5,77
| 5,77
5,84
| 5,84
5,91
| 5,91
5,98
| 5,98
6,05
| 6,05
6,12
| 6,12
6,19
| 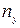
| | 515,5
522,5
|
|
|
|
|
|
|
|
|
|
| | 522,5
529,5
|
|
|
|
|
|
|
|
|
|
| | 529,5
536,5
|
|
|
|
|
|
|
|
|
|
| | 536,5
543,5
|
|
|
|
|
|
|
|
|
|
| | 543,5
550,5
|
|
|
|
|
|
|
|
|
|
| | 550,5
557,5
|
|
|
|
|
|
|
|
|
|
| | 557,5
564,5
|
|
|
|
|
|
|
|
|
|
| | 564,5
571,5
|
|
|
|
|
|
|
|
|
|
| | 571,5
578,5
|
|
|
|
|
|
|
|
|
|
| 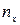
|
|
|
|
|
|
|
|
|
|
| 399.
| x
y
| 6,19
6,26
| 6,26
6,33
| 6,33
6,40
| 6,40
6,47
| 6,47
6,54
| 6,54
6,61
| 6,61
6,68
| 6,68
6,75
| 6,75
6,82
| 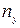
| | 578,5
585,5
|
|
|
|
|
|
|
|
|
|
| | 585,5
592,5
|
|
|
|
|
|
|
|
|
|
| | 592,5
599,5
|
|
|
|
|
|
|
|
|
|
| | 599,5
606,5
|
|
|
|
|
|
|
|
|
|
| | 606,5
613,5
|
|
|
|
|
|
|
|
|
|
| | 613,5
620,5
|
|
|
|
|
|
|
|
|
|
| | 620,5
627,5
|
|
|
|
|
|
|
|
|
|
| | 627,5
634,5
|
|
|
|
|
|
|
|
|
|
| | 634,5
641,5
|
|
|
|
|
|
|
|
|
|
| 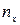
|
|
|
|
|
|
|
|
|
|
|
400.
| x
y
| 6,82
6,89
| 6,89
6,96
| 6,96
7,03
| 7,03
7,10
| 7,10
7,17
| 7,17
7,24
| 7,24
7,31
| 7,31
7,38
| 7,38
7,45
| 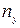
| | 641,5
648,5
|
|
|
|
|
|
|
|
|
|
| | 648,5
655,5
|
|
|
|
|
|
|
|
|
|
| | 655,5
662,5
|
|
|
|
|
|
|
|
|
|
| | 662,5
669,5
|
|
|
|
|
|
|
|
|
|
| | 669,5
676,5
|
|
|
|
|
|
|
|
|
|
| | 676,5
683,5
|
|
|
|
|
|
|
|
|
|
| | 683,5
690,5
|
|
|
|
|
|
|
|
|
|
| | 690,5
697,5
|
|
|
|
|
|
|
|
|
|
| | 697,5
704,5
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Тема: Кинематика поступательного и вращательного движения. 1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем
1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью...
Условия приобретения статуса индивидуального предпринимателя. В соответствии с п. 1 ст. 23 ГК РФ гражданин вправе заниматься предпринимательской деятельностью без образования юридического лица с момента государственной регистрации в качестве индивидуального предпринимателя. Каковы же условия такой регистрации и...
Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...
|
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
|
|

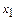 и
и 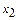 , причем
, причем 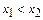 . Известны вероятность
. Известны вероятность 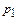 возможного значения
возможного значения 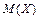 и дисперсия
и дисперсия 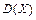 . Найти закон распределения этой случайной величины.
. Найти закон распределения этой случайной величины.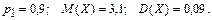
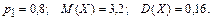
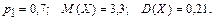
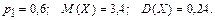
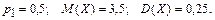
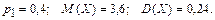
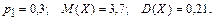
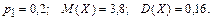
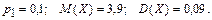
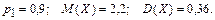
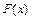 . Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
. Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.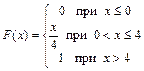
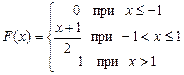
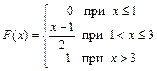
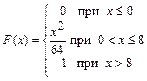
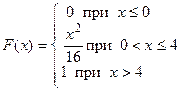
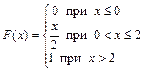
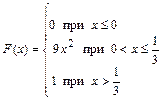
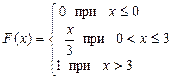
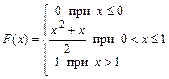
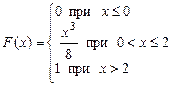
 382.
382. 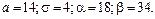
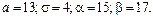 384.
384. 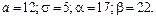
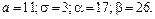 386.
386. 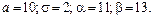
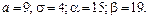 388.
388. 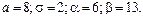
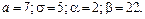 390.
390.