Интегралы
201 – 210. Найти неопределенные интегралы. В пп. «а» и «б» результаты проверить дифференцированием.
211 – 220. Вычислить несобственный интеграл или доказать его расходимость.
221. Найти площадь фигуры, ограниченной параболой 222. Найти площадь фигуры, ограниченной параболой 223. Найти длину дуги данной линии
224. Вычислить объем тела, образованного вращением вокруг оси O x кривой 225. Вычислить площадь фигуры, ограниченной 226. Вычислить длину дуги данной линии
227. Вычислить объем тела, образованного вращением вокруг Oх кривой 228. Найти длину кардиоиды 229. Вычислить объем тела, полученного вращением вокруг оси Оy фигуры, ограниченной парабалами 230. Найти длину дуги полукубической парабалы
Дифференциальные уравнения
231 – 240. Найти общее решение дифференциального уравнения.
251 – 260. Найти частное решение дифференциального уравнения
251. y'' – y' 252. y'' + y 253. y'' +7 y' +12 y = 254. y'' –2 y' = x 2–1; y (0) = 1, y' (0) = 1; 255. y''- 256. y'' + 9 y 257. y'' – 4 y' +8 y 258. y'' – 2 y' = 259. y '' +2 y ' +10 y 260. y'' – 6 y' +9 y =
261 – 270. Дана система линейных дифференциальных уравнений с постоянными коэффициентами
Найти общее решение системы.
261. 263. 265. 267. 269.
Кратные, криволинейные
|

 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
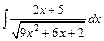 .
.
 ;
;
 ;
;
 ;
;
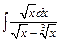 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
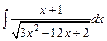 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
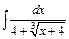 ;
;
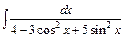 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
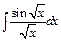 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
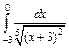 .
.
 ;
;
 .
.
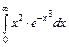 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 и прямой
и прямой 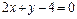 .
. и прямой
и прямой  .
. .
. , x = –1, y = 0.
, x = –1, y = 0.
 .
. , x = 0, y = 1.
, x = 0, y = 1. .
.
 , концами которой являются точки с абсциссами
, концами которой являются точки с абсциссами  и
и  .
. ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;

 ;
;
 .
.
 ;
;

 ;
;
 .
.
 ;
;
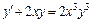 .
.
 ;
;
 .
.
 .
.
 .
.
 .
.
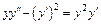 .
.
 .
.
 .
.
 .
.





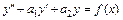 , удовлетворяющее начальным условиям y (0) = y 0,
, удовлетворяющее начальным условиям y (0) = y 0,  ;
;  ,
,  .
. ; y (0) = 4;
; y (0) = 4;  ;
; ; y (0) = 1, y' (0) = 1;
; y (0) = 1, y' (0) = 1; ; y (0) = 1, y' (0) = 1.
; y (0) = 1, y' (0) = 1. y (0) =
y (0) = 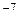 ; y' (0) = 0.
; y' (0) = 0. ; y (0) = 2, y' (0) = 3.
; y (0) = 2, y' (0) = 3. ; y (0) = 2, y' (0) = 2.
; y (0) = 2, y' (0) = 2. ; y (0) = 0, y' (0) =
; y (0) = 0, y' (0) =  .
. ; y (0)=1, y' (0)=3.
; y (0)=1, y' (0)=3. .
. ; 262.
; 262.  ;
; ; 264.
; 264.  ;
; ; 266.
; 266.  ;
; ; 268.
; 268.  ;
;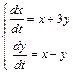 ; 270.
; 270.  ;
;


