Элементы линейной алгебры
51 – 60. Дана система линейных уравнений
Доказать ее совместность и решитьтремя способами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.
61 – 70. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
71 – 80. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 + z = 0.
Введение в математический анализ
81 - 85. Построить график функции
86 - 90. Построить график функции
91 – 100. Найти пределы функций, не пользуясь правилом Лопиталя.
91. a) в)
92. a) в)
93. a) в)
94. a) в)
95. a) в)
96. a) в)
97. a) в)
98. a) в)
99. a) в)
100. a) в)
101 – 110. Задана функция y = f (x) и два значения аргумента x 1 и x 2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
101. 102. 103. 104. 105. 106. 107. 108. 109. 110.
111 - 120. Задана функция y=f (x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
111.
113.
115.
117.
119.
|




























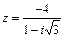




 преобразованием графика функции
преобразованием графика функции  .
.




 преобразованием графика функции
преобразованием графика функции  .
.




 ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
.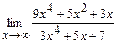 ; б)
; б)  ;
;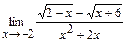 ; г)
; г)  ; д).
; д). 
 ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  .
. ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б) 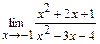 ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. , x 1 = 0, x 2 = –3.
, x 1 = 0, x 2 = –3. , x 1 = 0, x 2 = 2.
, x 1 = 0, x 2 = 2. , x 1 = 2, x 2 = 4.
, x 1 = 2, x 2 = 4. , x 1 = 1, x 2 = –1.
, x 1 = 1, x 2 = –1. , x 1 =4, x 2 = 6.
, x 1 =4, x 2 = 6. , x 1 = 1, x 2 = 3.
, x 1 = 1, x 2 = 3. , x 1 = 2, x 2 = 4.
, x 1 = 2, x 2 = 4. , x 1 = 1, x 2 = –1.
, x 1 = 1, x 2 = –1. , x 1 = 2, x 2 = 4.
, x 1 = 2, x 2 = 4. , x 1 = 1, x 2 = 3.
, x 1 = 1, x 2 = 3. ; 112.
; 112.  ;
; ; 114.
; 114.  ;
; ; 116.
; 116.  ;
; ; 118.
; 118.  ;
; ; 120.
; 120.  .
.


