Основные элементы алгебры логики
Анализ комбинационных устройств удобно проводить с помощью алгебры логики, оперирующей только с двумя понятиями: истинным В общем случае логическое устройство может иметь n входов и m выходов. Рассматривая входные сигналы х1, х2, …, хn в качестве аргументов, можно соответствующие выходные сигналы представлять в виде функции Функции алгебры логики (ФАЛ), иногда называемые переключательными функциями, обычно представляют в алгебраической форме (в виде математического выражения), например yi = (x 0 Ù x 1) Ú (x 1 Ù x 2), или в виде таблиц истинности (комбинационных таблиц). Таблица истинности содержит всевозможные комбинации (наборы) бинарных значений входных переменных с соответствующими им бинарными значениями выходных переменных; каждому набору входных сигналов соответствует определенное значение выходного сигнала - значение логической функции уi. Максимальное число возможных различных наборов (строк) зависит от числа входных переменных п и равно 2 п. В булевой алгебре выделяют три основные функции: конъюнкция, дизъюнкция, отрицание. Остальные функции являются производными от приведенных выше. Основные логические операции состоят из следующих элементарных преобразований двоичных сигналов: · логическое сложение или дизъюнкция, обозначаемое символом "Ú;" (или "+") и называемое также операцией ИЛИ. При этом число аргументов (слагаемых х) может быть любым. Эта операция для функции двух переменных x 1 и x 2 описывается в виде логической формулы
Это значит, что у истинно (равно 1), если истинно хотя бы одно из слагаемых x 1 или x 2. И только в случае, когда все слагаемые х равны 0, результат логического сложения у также равен 0. Условное обозначение, таблица истинности и другие показатели этой логической функции приведены во втором столбце табл. 1; · логическое умножение или конъюнкция, обозначаемое символом "Ù;" (или "×") и называемое также операцией И. При этом число аргументов (сомножителей х) может быть любым. Эта операция для функции двух переменных x 1 и x 2 описывается в виде логической формулы
Это значит, что у истинно (равно 1), если истинны сомножители x 1 и x 2. В случае, если хотя бы один из сомножителей равен 0, результат логического умножения у равен 0. Условное обозначение, таблица истинности и другие показатели логической функции И приведены в третьем столбце табл. 1; · логическое отрицание или инверсия, обозначаемое чёрточкой над переменной и называемое операцией НЕ. Эта операция записывается в виде
Это значит, что у истинно (равно 1), если х ложно (равно 0), и наоборот. Очевидно, что операция у выполняется над одной переменной х и её значение всегда противоположно этой переменной (см. четвертый столбец табл. 1).
Таблица 1
Основные логические операции ИЛИ, И и НЕ позволяют аналитически описать, а логические элементы ИЛИ (дизъюнктор), И (конъюнктор) и НЕ (инвертор) - реализовать комбинационное устройство любой степени сложности, т. е. операции В качестве примера рассмотрим функцию неравнозначности у двух переменных х 1 и х 2, принимающая значение 1 при х1 ¹ х2 и значение 0 при х 1 = х 2 = 0 или при х 1 = х 2 = 1, т. е. Примеры контактной и простейшей схемной реализаций дизъюнктора, конъюнктора и инвертора приведены в табл. 1.
|

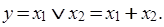

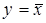 .
.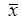
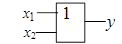




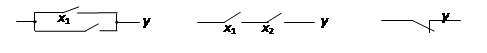 Контактная
Контактная

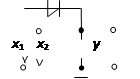









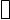






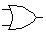


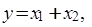
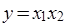 и
и  . Операцию неравнозначности чаще называют суммированием по модулю 2 и обозначают
. Операцию неравнозначности чаще называют суммированием по модулю 2 и обозначают 



