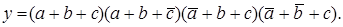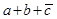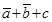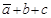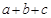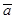Для построения логической схемы необходимо логические элементы, предназначенные для выполнения логических операций, располагать, начиная от входа, в порядке, указанном в булевом выражении.
Построим структуру логического устройства, реализующего логическую функцию трех переменных
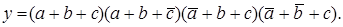




























































Слева располагаем входы
а,
b и
c с ответвлениями на три инвертора, затем четыре элемента ИЛИ и, наконец, элемент И на выходе (рисунок 1).
Итак, любую логическую функцию можно реализовать непосредственно по выражениям, представленным в виде СДНФ или СКНФ. Однако, полученная таким образом схема, как правило, не оптимальна с точки зрения её практической реализации: она громоздка, содержит много логических элементов и возникают трудности в обеспечении её высокой надёжности.
Алгебра логики позволяет преобразовать формулы, описывающие сложные высказывания с целью их упрощения. Это помогает в конечном итоге определить оптимальную структуру того или иного логического устройства, реализующего любую сложную функцию. Под оптимальной структурой принято понимать такое построение логического устройства, при котором число входящих в его состав элементов минимально.