Решение. 1. Вычертить геометрическую схему фермы, обозначив все узлы буквами A, B, C, D, E в масштабе 1:n (n = 1001. Вычертить геометрическую схему фермы, обозначив все узлы буквами A, B, C, D, E в масштабе 1:n (n = 100, 200, 250, 400) с указанием в узлах заданной нагрузки и направления опорных реакций VA, VB;
2. Определить опорные реакции фермы VA, VB VA = VB = Узловая нагрузка F/2 = где q - интенсивность равномерно-распределенной нагрузки; q = 5 l - длина панели фермы (расстояние между соседними узлами фермы) l =4м; 3. Обозначить внешние поля фермы a, b, c, d, е, f, k; 4. Обозначить внутренние поля фермы 1, 2, 3, 4, 5, 6, 7, 8; 5. Построить диаграмму; 5.1 Выбор масштаба сил: в 1 мм - 1 кН; 5.2 Построить многоугольник внешних сил. Так как эта система параллельных сил уравновешена, то замкнутый силовой многоугольник превращается в две накладывающиеся друг на друга вертикальные линии: Строим силовую линию а - b - с - d - e - f внешних сил, которые встречаются по обходу часовой стрелки, для этого откладываем вертикально вниз, от точки «а», в принятом масштабе отрезок (a - b), равный 10 мм и соответствующий силе От точки f строим силовую линию реакций связи (направленную вертикально вверх). Силу VB (f - k) направленную вертикально вверх откладываем от точки «f» до точки «k» (в принятом масштабе она соответствует отрезку 40 мм), соответственно силу VА (k – а) - от точки «k» до точки «а». В результате получаем замкнутый силовой многоугольник. 6. Построение диаграммы усилий.
|
= 
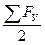2 
20 = 40 кН;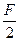
, приходящаяся на крайние узлы фермы определяется по формуле:
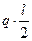= 5 ∙ 4/2 = 10 кН;
;
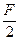, затем от точки «b», до точки «с» откладываем отрезок (b - c) равный 20 мм и соответствующий силе F, и так далее до точки f.
