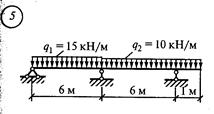
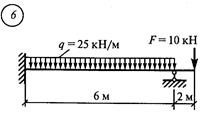
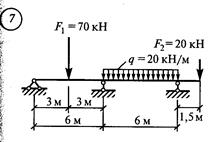
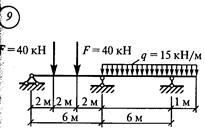
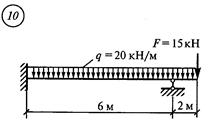
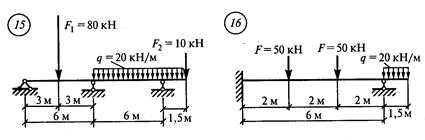
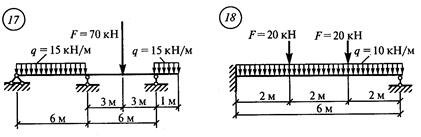
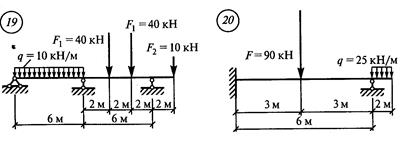
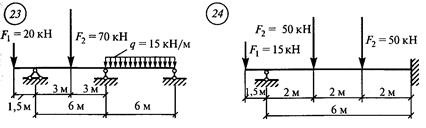
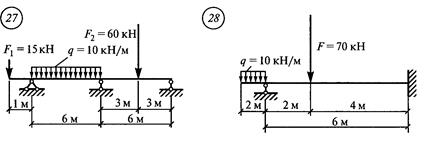
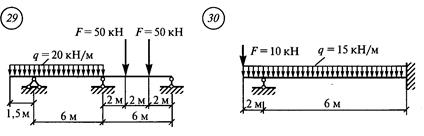
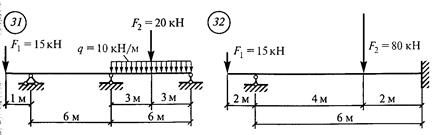
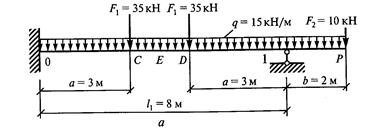
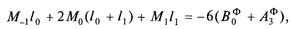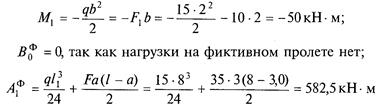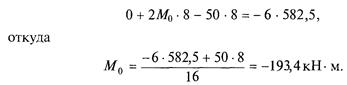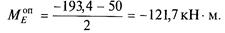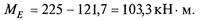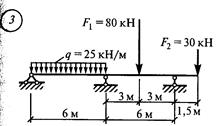
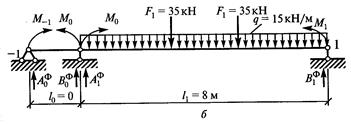
Решение. 1. Обозначить опоры 0, 1 и пролет 11 (рис1. Обозначить опоры 0, 1 и пролет 1 1 (рис. 43, а). 2. От заданной системы перейти к основной. Для этого вместо опор О и 1 вводим шарниры и опорные моменты М0 и М1. Кроме того, влево от опоры О вводим дополнительный (фиктивный) пролет 1 0 = О и фиктивную опору —1 с опорным моментом М-1 = О (рис. 43, 6). 3. Определить величины изгибающих моментов в характерных точках для основной схемы от заданной нагрузки (см. прил. 5). Моменты в точках С и D от силы F1
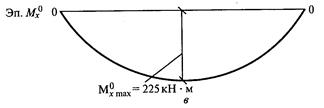
Момент в точке Е (середине пролета) от нагрузки q
Момент в точке Е от совместного действия силы F1 и нагрузки q равен сумме моментов от каждого из них:
рис. 43
Значения М 4. Составить уравнение трех моментов для промежуточной опоры 0:
где М-1 =0, так как и опора, и момент фиктивные; l 0 = 0, так как этот пролет тоже фиктивный;
Подставим числовые значения в уравнение трех моментов:
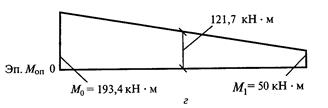
5. Построить эпюру опорных моментов Моп (рис. 43, г). Значение опорного момента в середине пролета (точка Е)
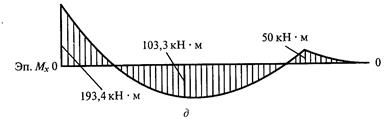
6. Определить значение изгибающего момента от заданной нагрузки для заданной схемы в точке Е:
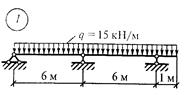
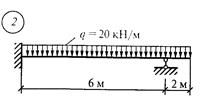
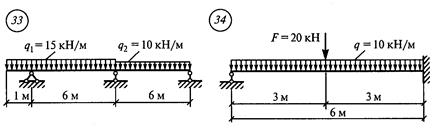
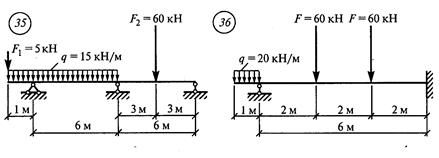
Строим эпюру Мх (рис. 43, д). Она должна быть уточнена после построения эпюры Qх, 7.По формулам ( см. методические указания ) вычислить поперечные силы в характерных точках. 8. По найденным значениям построить эпюру поперечных сил. Задание для расчетно-графической работы № 14. Построить эпюры изгибающих моментов и поперечной силы для неразрезной балки по данным одного из вариантов.
рис. 11
|
и М 
можно не определять, так как они меньше М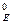 
. Строим эпюру М 
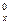(рис. 43, в).
