Методические указания. Для перекрытия нескольких пролетов могут использоваться простые балки (однопролетные с шарнирными опорами)
Для перекрытия нескольких пролетов могут использоваться простые балки (однопролетные с шарнирными опорами), неразрезные (статически неопределимые балки, имеющие непрерывное строение по всей своей длине с числом пролетов от двух и более) и многопролетные шарнирные балки. Многопролетная шарнирная балка - геометрически неизменяемая статически определимая система, составленная из расположенных в определенной последовательности однопролетных консольных или только одних консольных балок, соединенных между собой шарнирами. Преимущества шарнирных балок: · Нагрузки, действующие на консоли балок, являющихся составными частями шарнирной балки, уменьшают величины максимальных изгибающих моментов в ее пролетах, поэтому шарнирные балки требуют меньшего расхода материала по сравнению с простыми балками; · Неравномерное изменение температуры по высотешарнирных балок не вызывает в них дополнительных напряжений. Недостатки шарнирных балок: · Наличие шарниров усложняет изготовление и монтаж балок, обуславливает перелом упругой линии в местах установки шарниров, что при подвижной нагрузке вызывает толчки и удары; · Обрушение одного пролета шарнирной балки может вызвать обрушение других; · Устройство промежуточных шарниров требует дополнительных затрат. Для того, чтобы рассчитать многопролетную неразрезную балку, необходимо её разрезать на отдельные части в тех местах, где изгибающие моменты равны нулю, и соединить разрезные части шарнирами. Тогда многопролетная неразрезная статически неопределимая балка превратится в статически определимую. Каждый дополнительный промежуточный шарнир позволяет записать дополнительное управление статики - условие равенства нулю изгибающего момента в этом шарнире. Для того, чтобы шарнирная многопролетная балка была статически определимой, число промежуточных поставленных шарниров (Ш) должно равняться степени статической неопределимости (Л). Ш=Л=Н-3, где: Н - количество неизвестных опорных реакций; 3 - количество уравнений равновесия статики. При составлении схемы многопролетной шарнирной балки, имеющей геометрическую неизменяемость, статическую определимость, следует пользоваться правилами: 1. В каждом пролете можно устанавливать не более двух шарниров; 2. Пролеты с двумя шарнирами чередуются с пролетами без шарниров; 3. По одному шарниру может быть установлено в каждом пролёте, кроме одного. Схема взаимодействия (поэтажная схема) – схема, обеспечивающая наглядность, характер взаимодействия и порядок расчета элементов, составляющих многопролетную шарнирную балку. Схема взаимодействия может состоять из подвесной балки, передаточной и основной. Подвесной называют балку, шарнирно опирающуюся на концы консолей двух смежных с ней балок. Передаточной называют такую балку, давление от которой передается частично через опору на основание, а частично на консоль смежной балки, поддерживающей передаточную. Основной называют балку, которая передает давления от всех действующих на нее нагрузок через опоры на основание (землю). Равномоментные балки - балки, у которых наибольшие изгибающие моменты в пролетах равны по абсолютному значению моментам на опорах. Изгибающий момент Мх считается положительным, если в рассматриваемом сечении ось балки изгибается выпуклостью вниз (нижние волокна растянуты) и отрицательным если ось балки изгибается выпуклостью вверх. Ординаты эпюры М откладываются со стороны растянутых волокон («+» под основной линией) Поперечная сила в рассматриваемом сечении считается положительной, если её направление совпадает с вращением оставшейся части по ходу часовой стрелке. Положительные ординаты эпюры Q откладываются вверх от основной линии.
Пример. Определить внутренние силовые факторы, возникающие в шарнирной балке, построить эпюры Q и M, определить опасное сечение балки, подобрать размеры поперечного сечения, выполненного из стандартного прокатного профиля – двутавра, выполнить проверочный расчет. Исходные данные для своего варианта взять изтаблицы 5. 1. Вычертить схему с указанием размеров и нагрузки. Дано: F1 = 40 Кн; F2 = 20 Кн; F3 = 30 Кн; g=20
рис.26
1. Построить схему взаимодействия элементов Построение схемы взаимодействия начинают с замены поставленных шарниров на фиктивные опоры и деления шарнирной балки на основные и второстепенные (передаточные или подвесные) элементы, что позволяет выяснить, как происходит передача силовых воздействий от одной балки к другой. Данная балка состоит из двух основных балок (III и IV), подвесной балки I и передаточной II. Римскими цифрами намечен порядок их расчета с учетом взаимодействия. 2. Аналитический расчет шарнирной балки (рис.26) начинают с расчета подвесных балок, так как на них действуют только непосредственно приложенные к ним нагрузки. 2.1. Расчет балки I (рис.27):
рис. 27
2.1.1 Определение опорных реакций. В данном случае опорные реакции равны между собой: RC = RD = 2.1.3 Построение эпюры поперечных сил. Вычисляем для этого поперечные: силы в характерных сечениях: QС = RС = 40 кН; QD = Qc – q × 4 = 40 - 20´4 = - 4О кН; 2.1.4 Построение эпюры изгибающих моментов. Для простой балки, нагруженной равномерно распределенной нагрузкой, эпюра ограничивается квадратной параболой с максимальной ординатой по средине: Mmax= 2.2 Расчет балки П (рис.28)
рис. 28
2.2.1 Определение опорных реакций: ∑МH = 0 - RL×6 + F3×4 + F2×2 = 0, откуда:
∑M L = RH´6 - F2´4 - F3´2 = 0, откуда:
Проверка: ∑RY = RH - F2 - F3 + RL = 23,3 – 0 – 30 + 26,7 = 50 – 50 = 0, следовательно опорные реакции определены правильно. 2.2.2 Построение эпюр поперечных сил. Характерные точки (точки приложения сосредоточенных сил) исследуются слева и справа. Поперечную силу необходимо определить в сечении чуть левее точки приложения силы (Qлев) и в сечении чуть правее этой точки (Qпр):
2.2.3 Построение эпюр изгибающих моментов. Изгибающие моменты в характерных сечениях: МН = 0; МI = RH´2 = 23,3´2 = 46,6 кНм; МK = RL´2 = 26,7´2 = 53,4 кНм; МL = 0; 2.3. Расчёт балки ІІІ (с учётом давления на неё силы от балки І, в точке С равной и противоположно направленной опорной реакции Rс) (рис.29),
рис. 29 2.3.1 Определение опорных реакций: ΣМА = 0 - RВ´5+RС´7+q´7´3,5 = 0, откуда:
ΣМВ = 0 - RА´5 – q´7´1,5 + RС´2 = 0, откуда:
Проверка: ΣFу = RА – q´7 + RВ – RС = 26 - 20´7+154 – 40 = 0; 2.3.2 Построение эпюр поперечных сил. QA= RА = 26 кН.
QС = Для определения величины максимального изгибающего момента на этом участке необходимо найти расстояние X0 до сечения, в котором поперечная сила равна нулю. Приравняем нулю поперечную силу в этом сечении: QX0 = RА - q´X0 = 0, находим X0 = Х0 = 1,3 м. 2.3.3 Построение эпюр изгибающих моментов. Изгибающие моменты в характерных точках сечения: М(А) = 0; М(В) = RА´5 - q´5´ М(С) = 0. Изгибающий момент в произвольном сечение участка АВ на расстоянии X0 от точки А: М(Х0) = RА´1,3´ 2.4 Расчёт балки IV с учётом давления на неё силы от балки І, в точке D равной и противоположно направленной опорной реакции RD (рис.29), и давления силы в точке Н от балки ІІ, равной и противоположно направленной опорной реакции RН
рис. 30
2.4.1.Определение опорных реакций: ΣМЕ = 0 - RD´2 + F1´2,5 – RG´5 + RН´7 = 0 откуда:
ΣFу = 0 - RD + RE - F1 + RG – Rн = 0, следовательно RЕ = RD + F1 - RG + RН = 40 + 40 – 36,6 + 23,3 = 66,7 кН. RЕ = 66,7 кН. Проверка: ΣМG= - RD´7 + RE´5 - F1´2,5 + RH´2=-40 ´7 + 66,7´5 - 40´2,5 + + 23,3´2 = - 280 + 333,5 – 100 + 46,6 = 0. 2.4.2.Построение эпюры поперечных сил QD = - RD - 40 кН;
QH =
2.4.3 Построение эпюры изгибающих моментов. Изгибающие моменты в характерных сечениях:
МD = 0 кНм; МE = - RD´2 = - 40´2 = - 80 кНм; МF = - RD´4,5 +RE´2,5 = - 40´4,5 + 66,7´2,5 = - 13,3 кНм; МG = - R H´2 = - 23,3´2 = - 46,6 кНм; МH = 0 кНм.
2.5 Построение общей эпюры поперечных сил для всей шарнирной балки. Эпюры Q, полученные для отдельных балок, располагаем на одной оси, вычертив их в одном масштабе (см. рис. 1). 2.6. Построение общей эпюры изгибающих моментов для всей шарнирной балки. Эта эпюра (рис. 1) строится аналогично общей эпюре Q. 2.7. Определение Ммах = 120 кНм; 3. Определение момента сопротивления поперечного сечения Wx Wx = 4. Подбор размеров поперечного сечения двутавра. Используя таблицы сортамента, находим ближайшее большее или равное значение Wx, по нему определяем номер профиля Wx = 597см3, № 33. 5. Проверочный расчет. s = + Задание для расчетно-графической работы №10. Для шарнирной балки построить поэтажную схему, эпюры поперечных сил и изгибающих моментов. Подобрать поперечное сечение балки из двутавра. Исходные данные взять из табл. 5 и рисунка 31. Таблица 5
рис.31
|

 .
.

 =
=  = 40 кН;
= 40 кН;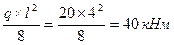

 кН.
кН. кН.
кН.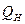 =
=  = 23,3 кН;
= 23,3 кН;  =
=  = 3,3 кН
= 3,3 кН =
=  =
=  =
= 
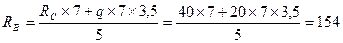 кН.
кН.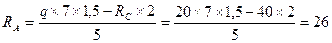 кН.
кН. = QA – q×5 = 26 – 20×5 = -74 кН;
= QA – q×5 = 26 – 20×5 = -74 кН; =
= 
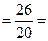 1,3 м.
1,3 м. = 26´5 - 20´5´
= 26´5 - 20´5´  = 26´1,3´0,65 = 16,9 кНм;
= 26´1,3´0,65 = 16,9 кНм;
 кН.
кН. = QD = - 40 кН;
= QD = - 40 кН; =
=  =
=  =
=  =
=  =
=  0,0005714 м3 = 571,4см3.
0,0005714 м3 = 571,4см3. = 201 ≤ 210 МПа
= 201 ≤ 210 МПа








