Использование рангового критерия Спирмена в решении различных задач.
Пример 1. В табл. 1 представлены n = 10 значений (xi, yi), i = Таблица 1.
Строим последовательность рангов (табл.2). По формуле (3) вычисляем реализацию статистики
Таблица 2
По таблицам распределения статистики
а квантили Пример 2: В определенном районе (площадью несколько сот квадратных километров) Большого Кавказского хребта имеются многочисленные рудные объекты разной величины. Как правило, они сопровождаются разломами земной коры разной глубины. Разломы можно находить геофизическими методами. Имеются основания предполагать, что рудные объекты связаны с этими разломами, причем чем более глубок разлом, тем большего размера могут быть сопровождающие его рудные объекты. Конечно, эта закономерность, если и действует, то лишь как тенденция. Подтвердить эту закономерность было бы очень полезно, так как она дает простое правило поиска месторождения. Попытаемся статистическими методами проверить это предположение. Выберем 10 наиболее крупных рудных объектов выделенного района и занумеруем их в порядке убывания. Таким образом, самый крупный объект получит номер 1, следующий по величине – 2, и т.д. Нумерация тех же объектов в порядке убывания глубины разломов иная, вот она: 3,1,2,6,4,5,9,8,10,7. Наше предположение о существовании связи между двумя признаками – размером объекта и глубиной разлома – чисто качественное. Довольно трудно сказать, насколько оно подтверждается сделанным наблюдением. Поэтому поступим иначе. Попробуем испытать (опровергнуть или нет) предположение, что никакой связи между признаками не существует. В таком случае вторая последовательность номеров не имеет никакой связи с первой. Вторая последовательность случайна по отношению к первой. Эту фразу мы возьмем за основу дальнейшего. Превратим нашу естественнонаучную гипотезу в статистическую: отсутствие связи между признаками будем истолковывать так, что вторая последовательность номеров есть результат случайного (в смысле теории вероятностей) эксперимента, в котором каждая нумерация имеет равную вероятность осуществления. Говоря подробнее, мы имеем в виду случайный эксперимент, состоящий в выборе перестановки чисел 1,2,…, 10. Вероятность надо задавать на множестве всех перестановок (которых довольно много – 10!=3628800). Наша статистическая гипотеза состоит из одного закона распределения – равномерного. Иначе говоря, гипотеза состоит в том, что все нумерации равновозможны. Теперь надо искать событие маловероятное, если гипотеза верна, и правдоподобное, если она не нарушена. Конечно, нарушаться гипотеза может более или менее сильно. Поэтому вероятность S должна быть тем больше, чем резче нарушена гипотеза. В нашем примере мы ждем нарушения гипотезы о случайности второй нумерации в сторону сходства нумераций. Ясно, что если бы вторая переменная совпала с первой, мы, пожалуй, не стали бы и сомневаться (насколько это правильно, мы обсудим в своем месте). Поэтому во множество S должна войти последовательность 1,2, …, 10 и близкие к ней. Близость между двумя перестановками х1, х2, …, хn и y1, y2, …, yn можно измерять различными способами. Часто для этого используют так называемый ранговый коэффициент корреляции ρ, по Спирмену. Он определяется так: В нашем примере первая последовательность неизменна, а может меняться только вторая. Так как вторая последовательность случайна, случайным оказывается значение ρ. Коэффициент ρ может принимать значения между -1 и +1. В случае если вторая нумерация выбирается чисто случайно, близкие к 1 (по абсолютной величине) значения ρ имеют малую вероятность. Типичные значения ρ лежат около нуля. Распределение коэффициента ρ при разных значениях n рассчитано. Его можно найти в специальных сборниках статистических таблиц. Как мы уже говорили, мы надеемся на проявление связи между двумя признаками, поэтому в качестве S мы должны взять событие вида {ρ>ρ0}. Величина ρ0 выбирается так, чтобы событие S при гипотезе имело малую вероятность (например, 0,01 или 0,005 или что-то подобное). В нашем случае ρ≈0,84, сумма квадратов равна 26. В таблицах находим, что значение суммы квадратов, меньшие или равные 32, имеют вероятность 0,0036. Следовательно, случайное значение p≥0,084 могло появиться лишь с вероятностью 0,0036, что практически невозможно. Это заставляет нас считать, что гипотеза независимости признаков опровергается имеющимися наблюдениями. Доказана, следовательно, положительная связь между глубиной разлома и размером месторождения. Попробуем теперь уменьшить объем наших наблюдений и ограничиться пятью месторождениями. Мы получили две последовательности: 12345 и 31254. Предполагая, что вторая нумерация чисто случайная, получаем, что каждая из 5! Перестановок имеет вероятность 1/120≈0,0083. В качестве события S можно предположить множество, состоящее только из одной последовательности 12345 (полное совпадение). Вероятность S при этом достаточно малая – как сказано, примерно 0,0083. Впрочем, при меньших значения n, например, при n=3даже полное совпадение нумераций не доказывает наличия закономерности. Если теперь при n=5 попытаемся увеличить S (с тем чтобы повысить чувствительность к нарушениям гипотезы, конечно, за счет некоторого увеличения вероятности отвергнуть гипотезу, если она верна), то в S надо будет включить последовательности, наиболее похожие на 12345. Ясно, что это – последовательности, содержащие одну перестановку номеров, т.е. 21345,13245,12435,12354. Теперь S состоит из пяти последовательностей. Вероятность его возросла до 5/120≈0,017. Если бы в нашем примере второй последовательностью оказалась одна из перечисленных, мы могли бы сделать осторожный вывод о наличии связи между признаками и предложили бы рассмотреть дополнительный материал. Впрочем, в нашем примере связь между признаками при n=5 не подтверждается. Это общая черта статистических методов – для их действия необходим достаточный объем наблюдений. Могло бы статься, что и при n=20 мы не обнаружили статистически значимой связи между признаками. Это означало бы, что сама связь невелика – тем слабее, чем больше наблюдений надо, чтобы ее обнаружить. (Конечно, точно сказать невозможно, что такое в данном случае «сила связи». Именно это заставило нас перейти к такой формулировке задачи, где это понятие не участвует). Поэтому не стоит чрезмерно увеличивать объем наблюдений – мы ведь собираемся использовать связь между признаками. Мы не можем это сделать, если эта связь слабая, т.е. признаки почти независимы. Пример 3. Два преподавателя оценили знания 12 учащихся по стобалльной системе и выставили им следующие оценки (в первой строке указанно количество баллов, выставленных первым преподавателем, а во второй – вторым): 98 94 88 80 76 70 63 61 60 58 56 51 99 91 93 74 78 65 64 66 52 53 48 62
|

 , непрерывной двумерной случайной величины (X,Y). Проверим на уровне значимости α = 0,05 гипотезу H0 о независимости случайных величин X и Y.
, непрерывной двумерной случайной величины (X,Y). Проверим на уровне значимости α = 0,05 гипотезу H0 о независимости случайных величин X и Y.

 рангового критерия Спирмена находим квантили
рангового критерия Спирмена находим квантили , (6),
, (6),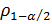 =
=  нет, так как
нет, так как  и Н0 не отклоняется даже на большем уровне значимости.
и Н0 не отклоняется даже на большем уровне значимости. . Здесь
. Здесь  – наибольшее возможное значение суммы квадратов. Поэтому ρ меняется от 1, когда нумерации совпадают, до – 1, когда они противоположны.
– наибольшее возможное значение суммы квадратов. Поэтому ρ меняется от 1, когда нумерации совпадают, до – 1, когда они противоположны.


