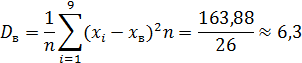Выборочная дисперсия
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения Выборочной дисперсией Если все значения х1, х2,..., хn признака выборки объема n различны, то
Если же значения признака х1, х2,…, хk имеют соответственно частоты n1,n2,…,nk, причем n1+n2+…+nk = n, то Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением. Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии: Пример 1. Выборочная совокупность задана таблицей распределения
Найти выборочную дисперсию. Решение. Найдем выборочную среднюю:
Найдем выборочную дисперсию:
Пример 2: По данной выборке определить выборочные среднее, дисперсию, уточненную дисперсию, среднее квадратическое отклонение (смещенное и уточненное).
|

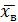 , вводят сводную характеристику— выборочную дисперсию.
, вводят сводную характеристику— выборочную дисперсию. называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 
 , т. е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
, т. е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.