По своему назначению и характеру решаемых задач статистические критерии чрезвычайно разнообразны. Однако их объединяет общность логической схемы, по которой они строятся. Коротко эту логическую схему можно описать так:
1. Выдвигается гипотеза 
2. Задаются величиной так называемого уровня значимости критерия α. Всякое статистическое решение, т.е. решение, принимаемое на основании ограниченного ряда наблюдений, неизбежно сопровождается некоторой, хотя, может и очень малой, вероятностью ошибочного заключение как в ту, так и в другую сторону. В какой-то небольшой доле случаев α гипотеза  может оказаться отвергнутой, в то время как на самом деле она является справедливой, или, наоборот, в какой-то небольшой доле случаев β мы можем принять нашу гипотезу, в то время как на самом деле она ошибочна, а справедливым оказывается некоторое конкурирующее с ней предположение – альтернативная гипотеза
может оказаться отвергнутой, в то время как на самом деле она является справедливой, или, наоборот, в какой-то небольшой доле случаев β мы можем принять нашу гипотезу, в то время как на самом деле она ошибочна, а справедливым оказывается некоторое конкурирующее с ней предположение – альтернативная гипотеза  . При фиксированном объеме выборочных данных величину вероятности одной из этих ошибок мы можем выбирать по своему усмотрению. Если же объем выборки можно как угодно увеличивать, то имеется принципиальная возможность добиваться как угодно малых вероятностей обеих ошибок α и β при любом фиксированном конкурирующем предположительном утверждении
. При фиксированном объеме выборочных данных величину вероятности одной из этих ошибок мы можем выбирать по своему усмотрению. Если же объем выборки можно как угодно увеличивать, то имеется принципиальная возможность добиваться как угодно малых вероятностей обеих ошибок α и β при любом фиксированном конкурирующем предположительном утверждении  . В частности, при фиксированном объеме выборки обычно задаются величиной α вероятности ошибочного отвержения проверяемой гипотезы
. В частности, при фиксированном объеме выборки обычно задаются величиной α вероятности ошибочного отвержения проверяемой гипотезы 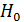 , которую часто называют «основной» или «нулевой». Эту вероятность ошибочного отклонения «нулевой» гипотезы принято называть уровнем значимости или размером критерия. Выбор величины уровня значимости α зависит от сопоставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери, тем меньшей выбирается величина α. Однако поскольку такое сопоставление в большинстве практических задач оказывается весьма затруднительным (часто трудно даже вообще сказать, в какую сторону ошибка является для нас более опасной), то, как правило, пользуются некоторыми стандартными значениями уровня значимости. К таким стандартным значениям можно причислить величины α=0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является величина уровня значимости α, равная 0,05. Она означает, что в среднем в пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу
, которую часто называют «основной» или «нулевой». Эту вероятность ошибочного отклонения «нулевой» гипотезы принято называть уровнем значимости или размером критерия. Выбор величины уровня значимости α зависит от сопоставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери, тем меньшей выбирается величина α. Однако поскольку такое сопоставление в большинстве практических задач оказывается весьма затруднительным (часто трудно даже вообще сказать, в какую сторону ошибка является для нас более опасной), то, как правило, пользуются некоторыми стандартными значениями уровня значимости. К таким стандартным значениям можно причислить величины α=0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является величина уровня значимости α, равная 0,05. Она означает, что в среднем в пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу 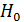 , при многократном использовании данного статистического критерия.
, при многократном использовании данного статистического критерия.
3. Задаются некоторой функцией от результатов наблюдения (критической статистикой)  . Эта критическая статистика
. Эта критическая статистика  , как и всякая функция от результатов наблюдения, сама является случайной величиной и в предположении справедливости гипотезы
, как и всякая функция от результатов наблюдения, сама является случайной величиной и в предположении справедливости гипотезы  подчинена некоторому закону распределения с плотностью
подчинена некоторому закону распределения с плотностью  .
.
4. Из таблиц распределения  находятся
находятся 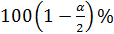 -ная точка
-ная точка  и
и 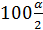 %- ная точка
%- ная точка  , разделяющие всю область мысленных значений случайной величины
, разделяющие всю область мысленных значений случайной величины  на три части: область неправдоподобно малых (I), неправдоподобно больших (III), и естественных или правдоподобных (в условиях справледливости гипотезы
на три части: область неправдоподобно малых (I), неправдоподобно больших (III), и естественных или правдоподобных (в условиях справледливости гипотезы  ) значений (II) (рисунок 1). В тех случаях, когда основную опасность для нашего утверждения представляют только односторонние отклонения, т.е. только «слишком маленькие» или только «слишком большие» значения критической статистики
) значений (II) (рисунок 1). В тех случаях, когда основную опасность для нашего утверждения представляют только односторонние отклонения, т.е. только «слишком маленькие» или только «слишком большие» значения критической статистики  , находят лишь одну процентную точку: либо
, находят лишь одну процентную точку: либо  -ная точка
-ная точка 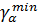 , которая будет разделять весь диапазон значений
, которая будет разделять весь диапазон значений  на две части: область неправдоподобно малых и область правдоподобных значений; либо
на две части: область неправдоподобно малых и область правдоподобных значений; либо 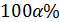 - ная точка
- ная точка  ; она будет разделять весь диапазон значений
; она будет разделять весь диапазон значений  на область неправдоподобно больших и область правдоподобных значений.
на область неправдоподобно больших и область правдоподобных значений.
5. Наконец, в функцию  подставляют имеющиеся конкретные выборочные данные
подставляют имеющиеся конкретные выборочные данные  и подсчитывают численную величину
и подсчитывают численную величину  . Если окажется, что вычисленное значение принадлежит области правдоподобных значений
. Если окажется, что вычисленное значение принадлежит области правдоподобных значений  , то гипотеза
, то гипотеза  считается не противоречащей выборочным данным. В противном случае делается вывод, что
считается не противоречащей выборочным данным. В противном случае делается вывод, что  на самом деле не подчиняется закону
на самом деле не подчиняется закону  и это несоответствие мы вынуждены объяснить ошибочностью высказанного нами предположения
и это несоответствие мы вынуждены объяснить ошибочностью высказанного нами предположения  и, следовательно, отказаться от него.
и, следовательно, отказаться от него.
Таким образом, решение, принимаемое на основании любого статистического критерия, может оказаться ошибочным как в случае отклонения проверяемой гипотезы  (с вероятностью α), так и в случае ее принятия (с вероятностью β). Вероятности α и β ошибочных решений называют также ошибками соответственно первого и второго рода, а величину 1 – β – мощностью критерия. Очевидно, из двух критериев, характеризующихся одной и той же вероятностью α отвергнуть в действительности правильную гипотезу
(с вероятностью α), так и в случае ее принятия (с вероятностью β). Вероятности α и β ошибочных решений называют также ошибками соответственно первого и второго рода, а величину 1 – β – мощностью критерия. Очевидно, из двух критериев, характеризующихся одной и той же вероятностью α отвергнуть в действительности правильную гипотезу  , следует предпочесть тот, который сопровождается меньшей ошибкой второго рода (или большей мощностью).
, следует предпочесть тот, который сопровождается меньшей ошибкой второго рода (или большей мощностью).

Рисунок 1. График плотности распределения критической статистики  и выделение областей «правдоподобных» (II) и «неправдоподобных» (I и III), в условиях справедливости гипотезы
и выделение областей «правдоподобных» (II) и «неправдоподобных» (I и III), в условиях справедливости гипотезы  , значений этой статистики.
, значений этой статистики.
Если проверяемое предположительное утверждение сводится к гипотезе о том, что значение некоторого параметра 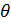 в точности равно заданной величине
в точности равно заданной величине  , то эта гипотеза называется простой. В других случаях гипотеза будет называться сложной.
, то эта гипотеза называется простой. В других случаях гипотеза будет называться сложной.


 . При фиксированном объеме выборочных данных величину вероятности одной из этих ошибок мы можем выбирать по своему усмотрению. Если же объем выборки можно как угодно увеличивать, то имеется принципиальная возможность добиваться как угодно малых вероятностей обеих ошибок α и β при любом фиксированном конкурирующем предположительном утверждении
. При фиксированном объеме выборочных данных величину вероятности одной из этих ошибок мы можем выбирать по своему усмотрению. Если же объем выборки можно как угодно увеличивать, то имеется принципиальная возможность добиваться как угодно малых вероятностей обеих ошибок α и β при любом фиксированном конкурирующем предположительном утверждении 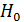 , которую часто называют «основной» или «нулевой». Эту вероятность ошибочного отклонения «нулевой» гипотезы принято называть уровнем значимости или размером критерия. Выбор величины уровня значимости α зависит от сопоставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери, тем меньшей выбирается величина α. Однако поскольку такое сопоставление в большинстве практических задач оказывается весьма затруднительным (часто трудно даже вообще сказать, в какую сторону ошибка является для нас более опасной), то, как правило, пользуются некоторыми стандартными значениями уровня значимости. К таким стандартным значениям можно причислить величины α=0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является величина уровня значимости α, равная 0,05. Она означает, что в среднем в пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу
, которую часто называют «основной» или «нулевой». Эту вероятность ошибочного отклонения «нулевой» гипотезы принято называть уровнем значимости или размером критерия. Выбор величины уровня значимости α зависит от сопоставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери, тем меньшей выбирается величина α. Однако поскольку такое сопоставление в большинстве практических задач оказывается весьма затруднительным (часто трудно даже вообще сказать, в какую сторону ошибка является для нас более опасной), то, как правило, пользуются некоторыми стандартными значениями уровня значимости. К таким стандартным значениям можно причислить величины α=0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является величина уровня значимости α, равная 0,05. Она означает, что в среднем в пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу  . Эта критическая статистика
. Эта критическая статистика  , как и всякая функция от результатов наблюдения, сама является случайной величиной и в предположении справедливости гипотезы
, как и всякая функция от результатов наблюдения, сама является случайной величиной и в предположении справедливости гипотезы  .
.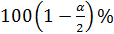 -ная точка
-ная точка  и
и 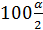 %- ная точка
%- ная точка  , разделяющие всю область мысленных значений случайной величины
, разделяющие всю область мысленных значений случайной величины  -ная точка
-ная точка 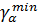 , которая будет разделять весь диапазон значений
, которая будет разделять весь диапазон значений 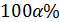 - ная точка
- ная точка  ; она будет разделять весь диапазон значений
; она будет разделять весь диапазон значений  и подсчитывают численную величину
и подсчитывают численную величину 
 и выделение областей «правдоподобных» (II) и «неправдоподобных» (I и III), в условиях справедливости гипотезы
и выделение областей «правдоподобных» (II) и «неправдоподобных» (I и III), в условиях справедливости гипотезы 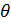 в точности равно заданной величине
в точности равно заданной величине  , то эта гипотеза называется простой. В других случаях гипотеза будет называться сложной.
, то эта гипотеза называется простой. В других случаях гипотеза будет называться сложной.


