Найти выборочный коэффициент ранговой корреляции Спирмена между оценками двух преподавателей.
Решение. Присвоим ранги Таблица 3.
Присвоим ранги
Таблица 4.
Напомним, что индекс i при у должен быть равен порядковому номеру оценки первого преподавателя. Найдем ранг у1. Индекс i=1 указывает, что рассматриваетсяоценка первого преподавателя, которая занимает в таблице 3 первое место (эта оценка равна 98); из условия видно, что второй преподаватель поставил оценку 99, которая в таблице 4 расположена на первом месте. Таким образом, у1=1. Найдем ранг у2. Индекс i=2 указывает, что рассматриваетсяоценка первого преподавателя которая занимает в таблице 3 второе место; из условия видно, что второй преподаватель поставил оценку 91, которая в таблице 4 расположена на третьем месте. Таким образом, ранг у2=3. Аналогично найдем остальные ранги: у3=2, у4=5, у5=4, у6=8, у7=6, у8=7, у9=12, у10=10, у11=9, у12=11. Выпишем последовательности рангов хi и уi: Таблица 5.
Найдем разности рангов: d1=x1-y1=0, d2=x2-y2=-1. Аналогично получим: d3=1, d4=-1, d5=1, d6=-2, d7=1, d8=1, d9=-3, d10=0, d11=2, d12=1. Вычислим суссу квадратов разностей рангов:
Найдем искомый коэффициент ранговой корреляции Спирмена, учитывая, что n=12:
Итак,
Пример 4: Специалисты двух заводов проранжировали 11 факторов, влияющих на ход технологического процесса. В итоге были получены две последовательности рангов: Таблица 6
Определить, согласуются ли мнения специалистов различных заводов, использую коэффициент ранговой корреляции Спирмена.
Решение:Выпишем последовательности рангов хi и уi:
Найдем разности рангов: d1=x1-y1=0, d2=x2-y2=0. Аналогично получим: d3=0, d4=-1, d5=1, d6=-3, d7=-1, d8=-3, d9=3, d10=3, d11=1. Вычислим суссу квадратов разностей рангов:
Найдем искомый коэффициент ранговой корреляции Спирмена, учитывая, что n=11:
Итак,
Пример 5: В примере 3 по выборке объема n=12 вычислен выборочный коэффициент ранговой корреляции Спирмена
Решение:Найдем критическую точку двусторонней критической области распределения Стьюдента по уровню значимости Найдем критическую точку:
Итак, Пример 6: В примере 4 по выборке объема n=11 вычислен выборочный коэффициент ранговой корреляции Спирмена Решение:Найдем критическую точку двусторонней критической области распределения Стьюдента по уровню значимости Найдем критическую точку:
Итак,
|

 оценкам первого преподавателя. Эти оценки расположены в убывающем порядке, поэтому их ранги
оценкам первого преподавателя. Эти оценки расположены в убывающем порядке, поэтому их ранги 
 оценкам второго преподавателя, для чего сначала расположим эти оценки в убывающем порядке и пронумеруем их:
оценкам второго преподавателя, для чего сначала расположим эти оценки в убывающем порядке и пронумеруем их: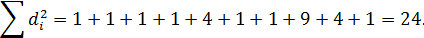


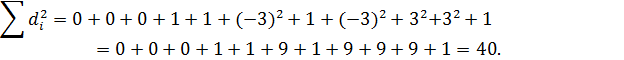


 и числу степеней свободы
и числу степеней свободы  ;
;  0,05;10)=2,23
0,05;10)=2,23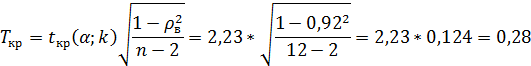
 . Так как
. Так как  -есть основания отвергнуть нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена. Другими словами, ранговая корреляционная связь между оценками двух преподавателей значимая.
-есть основания отвергнуть нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена. Другими словами, ранговая корреляционная связь между оценками двух преподавателей значимая. и числу степеней свободы
и числу степеней свободы  ;
; 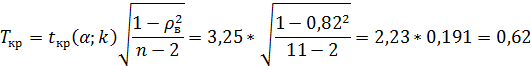
 . Так как
. Так как 


