Ранговый критерий Спирмена
Пусть имеется случайная выборка (X1,Y1),…,(Xn,Yn) генеральной совокупности двумерной непрерывной случайной величины (X, Y) с функцией распределения F(t,τ), a FX(t) и FY(τ) — функции распределения случайных величин X и Y соответственно. Если случайные величины X и У имеют нормальные распределения, то для проверки статистической гипотезы об их независимости H0: F(t,τ) = FX(t)FY(τ) можно использовать процедуру, связанную с вычислениями выборочного коэффициента корреляции (По формуле: Если же о распределениях непрерывных случайных величин X и Y ничего не известно, то для проверки основной гипотезы (1) при альтернативной гипотезе Н1: F(t,τ) ≠ FX(t)FY(τ) для некоторых (t, τ) € R2 используют ранговый критерий Спирмена, основанный на следующем понятии. Пусть задана конечная числовая последовательность (1) Определение 1. Рангом Ri элемента zi числовой последовательности (1) называют его порядковый номер в вариационном ряду z(1),…,z(N). Множество результатов измерений {x1, x2, …, xn} величины X называется выборкой объема n. Для того чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину X рассматривать как случайную величину, функцию распределения которой F(x)=P{X<x}следует определить. Полученный статистический материал x1, x2,...xn наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д. Если выборка объема n содержит k различных элементов Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы Согласно определению, Ri — это число элементов последовательности z1,..., zN, не больших чем zi, которое можно записать следующим образом: Ri = 1+ Пример 1. Рассмотрим выборку z4=(3,8, 4,7, —2,6,17,3). Ее вариационный ряд имеет вид —2,6; 3,8; 4,7; 17,3. Поэтому R1(z4) = 2, R2(z4) = 3, R3(z4) = 1, R4(z4) = 4. # Определение 2. Рангом элемента Zi случайной выборки ZN = (Z1,..., ZN) называют случайную величину Ri(ZN), реализация которой Ri(zN) есть ранг реализации zi случайной величины Zi, в вариационном ряду z(1),…,z(N). Обозначим через Ri = Ri(Xn) — ранг элемента Хi случайной выборки Х1,..., Хn, а через Si = Si(Yn) — ранг элемента Yi случайной выборки Y1,..., Yn. Ранговым коэффициентом корреляции Спирмена назовем случайную величину
где Статистика (2) является выборочным коэффициентом корреляции последовательностей рангов R1,…,Rn и S1,…,Sn. Согласно определению рангов Ri, Si, i=,
Без ограничения общности можно считать, что значения пар наблюдений (xi, yi), i =, занумерованы в порядке возрастания их первых элементов, т.е. так, что выполняются неравенства x1<x2<…<xn. В этом случае реализация ri ранга Ri равна i, i =, и значение
где Пусть выборочный коэффициент корреляции используется для нахождения линейной зависимости между случайными величинами X и Y. И если же между X и Y имеется функциональная, но не линейная зависимость, то выборочный коэффициент корреляции может быть равен нулю. Аналогично выгладит ситуация с ранговым коэффициентом (2), главным отличием является то, что он выявляет не только линейную, но и любую монотонную зависимость. Доказательство этого начнем с исследования статистики Если, а > 0, то большим значениям xi соответствуют большие значения yi, и, наоборот, меньшим значениям xi — меньшие значения yi, Если же, а < 0, то большим значениям xi соответствуют меньшие значения yi, а меньшим значениям xi — большие значения yi, i =. В этом случае ri=sn-i+1, si=rn-i+1, i =, и Заметим, что если Аналогично, если Y = Условие Рассмотрим теперь другой крайний случай, когда случайные величины X uY независимы, т.е. когда основная гипотеза H0 является истинной. В этой ситуации случайный вектор (Si,..., Sn) принимает с равной вероятностью любое свое возможное значение, являющееся одной из n! перестановок, составленной из чисел 1, 2,...,n. Следовательно, вероятность того, что статистика Можно показать, что при истинности основной гипотезы (1) M и, следовательно, при этом выборочные значения статистики При небольших n это распределение табулировано. Известно, что при n
т.е. квантили случайной величины
|

 , где
, где  - значение точечной оценки коэффициента корреляции).
- значение точечной оценки коэффициента корреляции). , причем
, причем 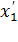 встречается mi раз, то число mi называется частотой элемента
встречается mi раз, то число mi называется частотой элемента  называется относительной частотой элемента
называется относительной частотой элемента 
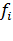 ).
). , где ŋ(t) — функция Хевисайда. Ранг любого элемента последовательности (1) — это натуральное число в диапазоне от 1 до N, причем ранг наименьшего элемента последовательности равен 1, а ранг наибольшего — N.
, где ŋ(t) — функция Хевисайда. Ранг любого элемента последовательности (1) — это натуральное число в диапазоне от 1 до N, причем ранг наименьшего элемента последовательности равен 1, а ранг наибольшего — N.

 и можно показать, что
и можно показать, что
 статистики
статистики  можно вычислить по формуле
можно вычислить по формуле
 — реализация ранга
— реализация ранга  , i =.
, i =. R, b
R, b  . Если пары наблюдений (xi, yi), i =, занумерованы по возрастанию первых элементов, то будут иметь место неравенства y1<y2<…<yn. Поэтому ri = si для всех i =, и из (4) следует, что
. Если пары наблюдений (xi, yi), i =, занумерованы по возрастанию первых элементов, то будут иметь место неравенства y1<y2<…<yn. Поэтому ri = si для всех i =, и из (4) следует, что  (х) — возрастающая функция, то ранг элемента xi в последовательности x1<x2<…<xn равен рангу
(х) — возрастающая функция, то ранг элемента xi в последовательности x1<x2<…<xn равен рангу  (x2)<…<
(x2)<…<  выполняется всегда, так как оно выполняется для выборочного коэффициента корреляции, а— это выборочный коэффициент корреляции, построенный по последовательностям рангов наблюдений.
выполняется всегда, так как оно выполняется для выборочного коэффициента корреляции, а— это выборочный коэффициент корреляции, построенный по последовательностям рангов наблюдений. примет любое из своих возможных значений
примет любое из своих возможных значений 
 где
где 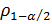 — квантиль уровня 1 —α/2 распределения случайной величины
— квантиль уровня 1 —α/2 распределения случайной величины  и при истинности основной гипотезы (1)
и при истинности основной гипотезы (1)



