Основные законы распределения
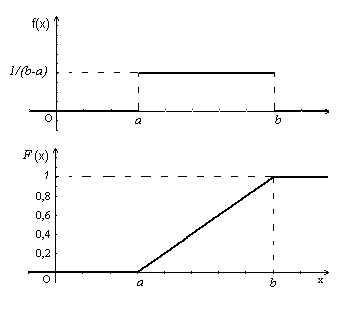
Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности f(x) случайной величины X постоянна, т.е. f(x) имеет вид:
Рисунок 1. Равномерный закон распределения Математическое ожидание равномерного распределения: M(X) = (a + b)/2 Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами a и σ, если ее плотность вероятности имеет вид:
Известно, что
Рисунок 2. График плотности случайной величины, в случае нормального распределения. Мода и медиана нормального распределения равны: Интегральная функция нормального распределения вероятностей:
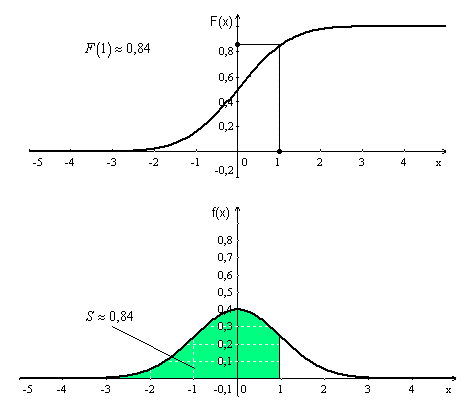
Интегральная функция распределения вероятностей показывает вероятность того, что случайная величина X примет значение меньшее, чем x: F(x) = P(X < x). Численно она равна площади криволинейной трапеции, ограниченной сверху графиком плотности вероятности, снизу осью абсцисс случайной величины, на интервале от -∞ до x. Ниже дана иллюстрация.
Рисунок 3. Интегральная функция нормального распределения.
Показательный (экспоненциальный) закон распределения. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ >0, если ее плотность вероятности имеет вид:
где λ — постоянная положительная величина. Математическое ожидание: Дисперсия: Используя свойство два плотности распределения (Несобственный интеграл от плотности распределения в пределах от -
Рисунок 4. Экспоненциальный закон распределения. Распределение хи-квадрат. Пусть независимые случайные величины Xi (i = 1, 2,..., n) — распределены по стандартному нормальному закону. Тогда говорят, что сумма квадратов этих величин
распределена по закону χ2 («хи квадрат») с n степенями свободы Плотность
Здесь Отсюда видно, что распределение «хи квадрат» определяется одним параметром n —независимым числом степеней свободы. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Рисунок 5. Распределение хи-квадрат. Основные характеристики распределение хи квадрат (математическое ожидание и дисперсия):
Распределение Стьюдента. Случайная величина
Распределение случайной величины
Математическое ожидание и дисперсия случайной величины, подчинённой распределению Стьюдента
Как и в случае и хи-квадрат распределением, при увеличении Распределение Фишера. Пусть случайная величина
Распределение случайной величины
Математическое ожидание случайной величины, подчинённой распределению Фишера,
Между случайными величинами, имеющими нормальное распределение: хи-квадрат, Стьюдента и Фишера, имеют место соотношения
|



 =M(X) и
=M(X) и  . График нормального распределения имеет куполообразную форму, он симметричен относительно своего математического ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения.
. График нормального распределения имеет куполообразную форму, он симметричен относительно своего математического ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения.


 .
. .
. до
до  экспоненциального закона:
экспоненциального закона:

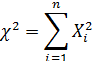
 распределения случайной величины χ2 имеет следующий вид:
распределения случайной величины χ2 имеет следующий вид:
 — гамма-функция.
— гамма-функция.

 есть отношение двух независимых случайных величин
есть отношение двух независимых случайных величин  и
и  , то есть
, то есть
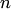 степенями свободы. Его плотность задаётся формулой
степенями свободы. Его плотность задаётся формулой
 , есть
, есть
 равна отношению двух независимых случайных величин
равна отношению двух независимых случайных величин  и
и  , то есть
, то есть
 и
и  степенями свободы. Оно имеет следующую плотность вероятности
степенями свободы. Оно имеет следующую плотность вероятности
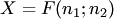 определяется по формуле
определяется по формуле




