Определение и примеры независимых случайных событий и случайных величин
Два случайных события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями. Пример 1. Монета брошена два раза. Вероятность появления "герба" во втором испытании (событие В) не зависит от появления или не появления "герба" в первом испытании (событие А). В свою очередь, вероятность наступления события А не зависит от наступления или ненаступления события В. Таким образом, события Случайной называют величину, которая при каждом испытании принимает одно и только одно из возможных значений, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Пример 2. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,..., 100. Пример 3. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). Будем далее обозначать случайные величины прописными буквами латинского алфавита X, Y, Z…, а их возможные значения—соответствующими строчными буквами х, у, z, …, х1, х2,... Например, если случайная величина X имеет три возможных значения, то их можно обозначить так: х1, х2, х3. Формальное математическое определение следующее: пусть Случайные величины классифицируют на дискретные и непрерывные. Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью. Соотношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины. В отличие от дискретной случайной величины непрерывные случайные величины невозможно задать в виде таблицы ее закона распределения, поскольку невозможно перечислить и выписать в определенной последовательностей все ее значения. Одним из возможных способов задания непрерывной случайной величины является использование функции распределения. Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия. Закон распределения непрерывной случайной величины нельзя задать так же, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю. Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий (Х=х) для разных х, а вероятности события (Х<х). При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:
Функцию распределения F(x) называют также интегральной функцией распределения или интегральным законом распределения. Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины, т. е. представить некоторую замену вероятностям pi для дискретной случайной величины в непрерывном случае. Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения:
|

 и
и  независимые.
независимые. — вероятностное пространство, тогда случайной величиной называется функция
— вероятностное пространство, тогда случайной величиной называется функция  , измеримая относительно
, измеримая относительно  и борелевской σ - алгебры на
и борелевской σ - алгебры на 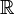 . Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением.
. Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением. .
. .
.


