Розрахунок центрально стиснутих елементів
Центрально стиснуті елементи поділяють на короткі і довгі гнучкі. Короткі – це елементи, довжина яких перевищує найменший поперечний розмір не більше, ніж в 5 разів. Довгі – відповідно більше, ніж в 5 разів. Центрально стиснуті стержні розраховуються за І групою граничних станів. Їх несуча здатність може бути вичерпана внаслідок настання одного з двох граничних станів: 1) втрати міцності, коли руйнується матеріал елемента (для коротких стержнів); 2) втрати стійкості, коли порушується прямолінійна форма елемента без механічних пошкоджень матеріалу (для довгих стержнів). Короткі стиснуті стержні, як і розтягнуті, розраховуються на міцність за формулою:
Де А – площа перерізу “брутто”. В будівельній практиці короткі стержні зустрічаються надзвичайно рідко, і в основному ми маємо справу з довгими стержнями, несуча здатність яких обмежується не внаслідок втрати міцності, а в результаті втрати стійкості. Довгі стиснуті стержні розраховуються за умовою стійкості. Проблема стійкості стальних конструкцій має виключно важливе значення – біля 40% аварій МК виникає внаслідок її недооцінки. Суть проблеми стійкості полягає в наступному. Якщо пружний стержень стискувати центрально прикладеною силою N, то, доки сила мала, прямолінійна форма рівноваги стійка. Якщо навіть відхилити стержень від положення рівноваги невеликою боковою силою, то після її зняття стержень відновить свою прямолінійну форму. При зростанні сили N наступить момент, коли робота, що здійснюється силою при пружному переміщенні Поздовжня сила, яка відповідає моменту переходу стержня з прямолінійного в криволінійний стан рівноваги, називається критичною силою Nсr. Згин, який виникає від дії центрально прикладеної поздовжньої сили, називається поздовжнім згином. Формула для визначення напружень в цьому випадку приймає вигляд:
де sсr – критичні напруження, що відповідають критичній силі,
Формула критичної сили для стержня з шарнірним закріпленням кінців при центральному стиску була отримана в 1744 р. Леонардом Ейлером:
де Е – модуль пружності; Іmin – мінімальний момент інерції перерізу; lef – розрахункова довжина стержня. Вона характеризує не тільки його протяжність, але й форму, яку приймає стержень при втраті стійкості; lef = m l; m - коефіцієнт приведення розрахункової довжини, який залежить від умов закріплення кінців стержня; l - геометрична довжина стержня, рівна найменшій відстані між точками закріплення стержня від поперечного зміщення. Покажемо основні 4 випадки опорних закріплень стержнів (рис.4.4). З рисунка видно, що стержні, які мають однакову геометричну довжину, будуть мати різні розрахункові довжини. За допомогою коефіцієнта m стержень при любому закріпленні кінців приводиться до основного випадку – до елемента з шарнірним закріпленням кінців, для якого справедлива формула критичної сили Ейлера. Підставимо значення критичної сили в формулу критичних напружень:
Враховуючи, що Згадуючи поняття гнучкості
отримуємо кінцеву формулу Ейлера для sсr:
тобто sсr залежить від l. Оскільки умова зберігання стійкості стержня s £ sсr, то для підвищення несучої здатності стержня необхідно намагатися збільшити sсr, а це можливо при зменшенні гнучкості l. Слід звернути увагу на те, що особливий ефект дає збільшення несучої здатності стиснутих стержнів не за рахунок нарощування площі перерізу, а за рахунок використання більш раціональної його форми. Такими перерізами є, наприклад, тонкостінні круглі або квадратні труби, для яких характерні великі моменти інерції при мінімальних площах перерізу. Оскільки гнучкість l зменшується при збільшенні радіуса інерції перерізу і, то слід використовувати профілі, для яких характерні великі радіуси інерції при мінімальних площах перерізу. Це особливо стосується кутиків. Порівняємо для прикладу характеристики кутиків Ð90х9 і Ð100х8 (рис. 4.5).
З порівняння видно, що площі поперечного перерізу обох кутиків однакові, але у кутика Ð100х8 (з більш розвинутими полицями і при меншій їх товщині) радіус інерції значно більший, а отже цей кутик ефективніший при роботі на стиск. З виразу (1) для s сг видно, що критичні напруження не залежать від міцності сталі. Два однакових стержня, виготовлених із сталі звичайної міцності і високоміцної сталі, будуть втрачати стійкість при однаковому навантаженні. А тому використання високоміцних сталей в стиснутих стержнях не раціонально. Чи завжди справедлива формула Ейлера для sсr? Вона справедлива лише при постійному значенні модуля пружності, а Е=const лише на прямолінійному відрізку діаграми (від т.0 до т.1, див. рис.2.2). Точці 1 відповідає напруження, яке називається межею пропорційності Отже формула справедлива до тих пір, доки
Звідси неважко визначити те мінімально можливе значення гнучкості, при якому справедлива формула Ейлера. Для сталі Ст3
Отже, формула Ейлера справедлива лише при l > 101. Але, як правило, елементи МК мають меншу гнучкість, і значення критичних напружень, якщо їх підрахувати за формулою Ейлера, будуть неправильними і значно завищеними (помилка десятикратна і не в сторону запасу міцності). Цю ситуацію виправили, ввівши поняття зведеного модуля пружності Т. Тоді формула для критичних напружень приймає вигляд:
Залежність Т від l має вигляд, наведений на рис.4.6. Ця формула є наближеною, але дає достатнє співпадання з дослідами по розрахунку критичних напружень, при цьому для гнучкості l»0…100 модуль пружності Т приймає змінні значення (див. графік), а при l > 100 – постійне значення Е = 2,06 · 105 МПа. В практичних розрахунках обчислюються не sсr, а значення їх відношень до Ry:
Величину цього відношення j називають коефіцієнтом поздовжнього згину. Записане відношення – це фізичний смисл коефіцієнта j. Оскільки стиснутий стержень втрачає стійкість раніше, ніж метал досягає межі текучості, то це означає, що sсr < Ry. Тоді очевидно, що завжди j < 1. Для коротких стержнів може виявитися, що sсr > Ry, і тоді формально j>1. Але це означає, що несуча здатність стержня вичерпується не стійкістю його форми, а міцністю металу, і розрахунок слід виконувати за умовою міцності. Слід також мати на увазі, що в практиці будівництва не існує ідеальних центрально стиснутих стержнів. В елементах реальних конструкцій завжди виникають, хоча і невеликі, випадкові ексцентриситети, які впливають на їх роботу. Походження цих ексцентриситетів різноманітне: ними можуть бути ексцентриситети в прикладанні навантаження, початкові викривлення елементів і т.ін. А це означає, що з самого початку роботи елемента в ньому крім поздовжнього зусилля N виникає, хоча і невеликий, згинаючий момент М. І по суті розрахунок центрально стиснутих елементів являє собою розрахунок позацентрово стиснутих елементів з малими ексцентриситетами. Вплив випадкових ексцентриситетів на роботу стиснутих елементів оцінюється методами математичної статистики і також враховується коефіцієнтом j. З введенням в розрахунок коефіцієнта j умова стійкості приймає вигляд:
Кінцева робоча формула має вигляд:
Це і є умова стійкості центрально стиснутого елемента. Коефіцієнт j залежить від l і Ry. Оскільки закріплення стержня в різних площинах може бути різне, то коефіцієнт j обчислюють, як правило, в такій послідовності: le f, ,x = mх l le f ,y = my l;
По більшому з двох значень гнучкості lmax і величині Ry визначають j за таблицею 72 або за формулами СНиП. Гнучкість центрально стиснутих елементів обмежується граничною гнучкістю, яка наведена в СНиП для різних елементів конструкцій (табл.19): l £ lu. Гранична гнучкість lu має плаваючі значення і для більшості стиснутих стержнів lu = 120…150. На центральний стиск можна розглядати три типи задач, аналогічних центральному розтягу.
|

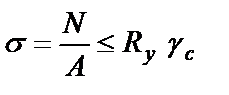
 , перевищить потенційну енергію пружної деформації стержня, і прямолінійний стан стає нестійким. Поряд із стиском з’являється нова форма деформації – згин (рис.4.3).
, перевищить потенційну енергію пружної деформації стержня, і прямолінійний стан стає нестійким. Поряд із стиском з’являється нова форма деформації – згин (рис.4.3). ,
, .
. ,
, .
. , отримаємо:
, отримаємо:  .
. ,
, , (1)
, (1) .
. .
. , Е=2,06 ·105 МПа. Тоді, прирівнявши критичні напруження до межі пропорційності, отримаємо:
, Е=2,06 ·105 МПа. Тоді, прирівнявши критичні напруження до межі пропорційності, отримаємо: звідси
звідси 
 .
. .
. .
.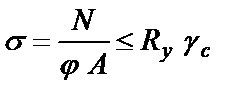 .
.




