Определение работы суммарного приведенного момента сил.
Известно,что для модели справедливо следующее соотношение:
Воспользуемся методом графического интегрирования. На графике момента делим ось абсцисс на 12 интервалов по π/6 каждый. В пределах каждого интервала подынтегральную функцию определяем с помощью равновеликого по площади прямоугольника, заменяющего на данном интервале криволинейную трапецию. Среднее значение ординаты y*Mi на данном интервале соответствует среднему значению суммарного приведенного момента. Отрезки проецируем на ось ординат, и полученные точки соединим с началом отрезка К=40мм, который был отложен слева от нуля на графике моментов. Таким образом получили ряд лучей наклоненных под углами ψ1, ψ2,…, ψ12 к положительному направлению оси абсцисс. На графике работы последовательно проводим лучи под углом ψ1, ψ2,…, ψ12, каждый из которых соответствует определенному интервалу. При этом построении имеет место определенная зависимость между масштабами:
С целью уменьшить высоту графика по оси ординат выбираем масштаб:
После нахождения отдельных значений искомой функции, в конце интервалов полученные точки аппроксимируем плавной кривой это необходимо сделать, так как подынтегральная функция является непрерывной.
Таблица 1.6 Сумма работа в различных положениях механизма.
1 .7 Определение угловой скорости начального звена кривошипно-ползунного механизма.
Зависимость угловой скорости начального звена 1 как функция обобщенной координаты:
Имея графики суммарной работы и суммарного приведенного момента, для каждого положения начального звена вычислим его угловую скорость и построим график ω1(φ1).
Таблица 1.7 Угловая скорость в различных положениях механизма.
Выбираем масштабы:
|
.
.
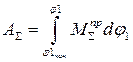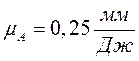
, Дж
, где
- кинетическая энергия звеньев в начальном положении,Дж. 
=0 (из условия), поэтому 
=0.
- суммарный приведенный момент инерции звеньев механизма.
.
